This paper was first presented at GPD 2019 by Dr. Mikko Rantala from Glaston Finland Oy.
Abstract
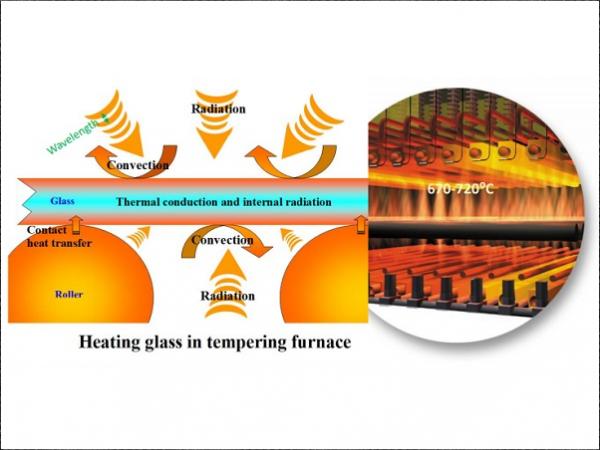
In a tempering furnace, glass is placed on top of rotating ceramic rollers, where it is exposed to radiation emitted by radiant heaters, rollers and other surfaces inside the furnace. Convection heat transfer between hot air jets and the glass affects both glass surfaces. On the lower surface, also contact heat transfer between the glass and rollers takes place.
There is quite a wide range of different tempering furnace models on the market with differing devices for implementing radiation and convection heat transfer. In this paper, the basics of the heat flux modes are given, a solution method for the glass energy equation is introduced, and some tempering furnaces are theoretically studied to show the portions of the heat transfer phenomena inside furnaces during heating.
1. Introduction
Glass tempering is a process in which the strength of float glass is improved with heat treatment. In a tempering furnace, glass is placed on top of rotating ceramic rollers. During the tempering process, glass plates are heated to about 640°C and then cooled by air jets at a cooling rate depending on glass thickness. In an ideal heating process, the heat transfer rate to glass is the same via the top and bottom sides, so that the thicknesswise temperature profile generated to the glass during heating is symmetrical. After heating, i.e. just before quenching, the glass temperature should be the same throughout the whole glass surface area, and the same in all glass sheets in a glass loading in a furnace. The capability of a furnace to approach such an ideal heating process clearly depends on the furnace model.
In the simplest tempering furnaces, the heating of glass is based on thermal radiation exchange between resistors and glass, and in addition to radiation also natural convection and contact heat transfer from rollers to glass occurs. Such furnaces are becoming very rare on the market due to demands related to tempering of low-e coated glass. Low-e coated glass surface can reflect as much as 96% of the thermal radiation emitted by a furnace’s hot surfaces. With forced convection, heating of the coated top side of the glass can be intensified to keep the thickness-wise temperature profile symmetrical, i.e. glass flat in the furnace. Forced convection is arranged with air jets, which are focused to impinge on the glass surface. Forced convection is used together with radiation to intensify heat transfer even for clear glass.
The spokespersons of the different furnace manufactures have various of beliefs and opinions about the convection capability in the furnace models they represent. This paper aims to clarify these issues. In the paper, three furnace models are theoretically studied to solve the portions of their internal heat transfer phenomena.
2. Various types of tempering furnaces on the market
There is quite a wide range of different tempering furnace models on the market, each device differing in their creating, focusing and controlling radiation and convection heat transfer. A quite typical heating speed for clear glass is 40 s/mm times glass thickness in mm, which varies slightly depending on glass thickness and furnace model. The heating time of low-e coated glass is longer and much more dependent on furnace model.
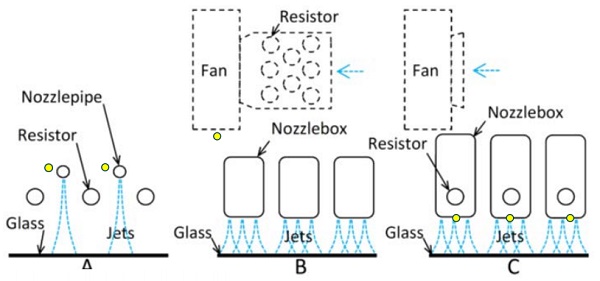
Top heaters inside the furnace are often open coils electric resistors radiating heat directly toward to glass (see type A in Figure 2.1). Bottom-side open coil heaters have thin steely covers to protect them against broken glass. The direct radiation from the bottom resistors, or from the covers to be exact, to the glass is relatively quite low due to the narrow gap between rollers.
Thus, the main radiation heat transfer path to glass on the bottom side is that the bottom resistors radiate to the rollers and the rollers radiate to the glass. Radiation heat transfer from hot surfaces inside the furnace to glass depends on the surface radiative properties and temperatures. Radiative properties of hot surfaces, i.e. resistors, rollers, walls and nozzle boxes, does not represent much variation depending on furnace model, but their relative surface area the glass can see varies.
However, radiation heat transfer rate differences in furnaces depend mainly on the furnace set temperatures. They also depend slightly on where thermocouples measuring local furnace temperatures are located and how the system controlling these temperatures is programmed. A typical set value for a furnace temperature is between 670 and 720°C. A higher value gives more heating speed, but it also unavoidably causes more variation in glass local and average tempering temperatures. Heating stays better in balance, when the same set temperatures can be used for the top and bottom side heaters in heating recipes.
There are two different technologies used to implement convection in tempering furnaces: external-air convection and circulatedair convection. In external air convection, pressurized fresh air coming from outside the furnace is blown toward the glass through holes in convection pipes. External air convection is also called air aspiration convection or flow-through air convection because the same amount of air blown into a furnace is also blown out of the furnace.
Usually, air is pressurized with a compressor to about 8 to 12 bars and over pressure inside a convection pipe, i.e. blowing pressure is set between 0 and 4 bars depending on the heating recipe. The blowing pressure is controlled with valves located outside of the furnace. The typical diameter of a blowing hole is 1–2 mm and 10–80 holes are inside one furnace square metre.
Such a convection is called compressed air convection. This may even be the only method to arrange external air convection, but it is very possible that some furnace manufactures are trying to avoid clear violation of the patent [2A] by using fans or turbo fans instead of a compressor for feeding fresh air to the blowing holes on the bottom side of the glass plate.
In circulating air convection technology, air is drawn by fans inside the furnace, guided to blowing holes, and blown toward the glass. Thus, external air feed into a furnace is avoided. The convection rate is controlled by changing the rotation speed of a fan impeller with a frequency controller, which changes the blowing pressure. In the simplest circulating air convection systems, convection pipes or nozzle boxes are placed between, above or below the heating resistors.
In such a design, air temperature is not controlled, and it drops strongly at the beginning of the heating depending on the loading degree. Air temperature is much more stable when the resistors are located in the main air feeding channel (see type B, Figure 2.1) or inside nozzle boxes (type C, Figure 2.1), because air is forced to flow through the resistors. The resistors located in the air feeding channel first transfer heat mainly to air, and then heat is transferred from the air to the glass.
Such a system with a thermocouple in the main air feeding channel offers well-controlled air temperature, but radiation toward the glass is without any control. Thus, temperatures of surfaces radiating to the glass drop strongly at the beginning of heating. Circulating air convection systems with open coil resistors inside nozzle boxes are often controlled with thermocouples mounted to the surface of nozzle boxes toward the glass, which offers precise control of radiation heat transfer.
The surface temperature of the nozzle box and the thermocouple decreases when cold glass comes into its range. Then, the resistor inside nozzle box switches on and the temperature soon starts decreasing back to a set value. The resistor also heats up the air blasted against the glass at its range. Thus, both radiation and convection are controlled with the same resistor. In a circulating air convection system, the diameter of a blowing holes is typically between 5 and 15 mm, 100 to 400 holes are within one square meter of the furnace and the blowing pressure is between 100 and 1000 Pa.
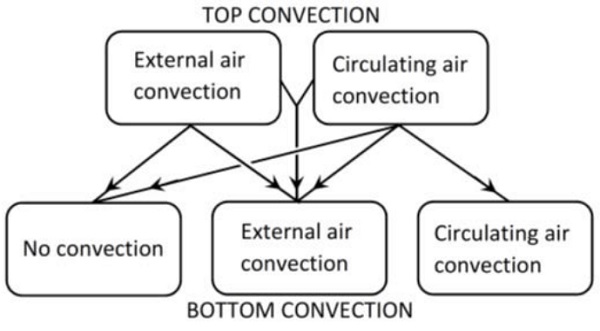
Particularly when low-e coated glasses are heated, the convection heat transfer rate must be much higher on the top side than on the bottom side. Circulating air convection is typically stronger than external air convection, but a circulating air convection system clearly costs more. This fact has been considered in furnaces where circulating air convection occurs on the top surface of the glass and compressed air convection occurs on the bottom [2A].
Such a solution is close to optimal because bottom convection is a good tool to for keeping glasses flat during the early stages of heating, which often succeeds in a quite low convection rate. Figure 2.2 shows the rest of the top and bottom convection combinations available on the market. The latest new combination has both circulating and external air convections on the top side and external air convection on the bottom side. Sometimes the combination with top and bottom circulating air convection is referred to as full convection, which easily gives the wrong impression of the convection rate in such a furnace.
The naming of convection systems is quite nonconventional among furnace manufacturers, even though there are only two technologies and some combinations of them. On the other hand, this is understandable because the capability of different circulated-air convection systems, as well as external air convection systems, differs.
3. Heat transfer phenomena in tempering furnaces
3.1 Thermal radiation
In Figure 3.1, the behaviour of incident radiation hitting a glass plate is shown schematically. At the air-glass interface, a proportion of the radiation is reflected. The reflectivity ρ depends on the hitting angle and the wavelength [1]. Because of the low reflectivity (typical direction-averaged value is 0.09) of a clear glass surface, the main proportion of radiation goes through the interface. Then, the radiation to which glass is opaque is absorbed to the glass surface. The radiation to which glass is transparent penetrates deeper into the glass, and a proportion of it is absorbed into the glass. The rest of the radiation meets the glass-air interface, where a second reflection occurs.
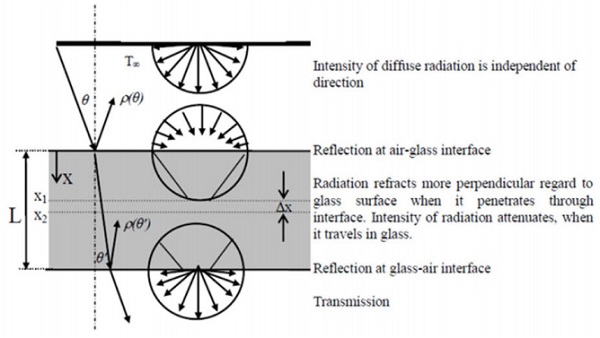
Due to absorption, the intensity of the radiation attenuates when it propagates in glass. The intensity of radiation after a path distance x in a medium is

where i0 is the intensity at the surface and κ is the absorption coefficient. Soda-lime glass has two cut-off wavelengths, at which its absorption coefficient undergoes a major change. Practically speaking, glass is opaque for thermal radiation when the wavelength is over 4.5 µm, whereas for wavelengths under 2.75 µm, glass is very transparent.
At wavelengths between 2.75 and 4.5 µm, the absorption coefficient is about 4 cm-1, which is still a relatively high value. At wavelengths between 1 and 2.75 µm, the absorption coefficient is about 0.3 cm-1. The spectral absorptance of clear 4 mm-thick glass is 0.77, i.e. 77% from the incident radiation, when κλ = 4 cm-1, and 0.12, when κλ = 0.3 cm-1. The direct absorption of radiation by the glass interior is capable of decreasing the thermal shock in the glass at the beginning of the heating [3].
Low-e coating on a glass surface is like a radiation-reflecting mirror for the incident radiation in a tempering furnace. The radiative properties of some low-e coatings are given with details in [1], from which the following main points are chosen. A low-e coating changes glass surface reflectivity selectively. For visible light (0.4 < λ < 0.7 µm), reflectivity remains almost constant, but at slightly longer wavelengths, reflectivity increases sharply to 0.8 – 0.98, depending on the coating. The coating itself also absorbs radiation and the spectral absorptivity increases slightly with temperature.
With the directional spectral reflectivity, spectral absorption coefficient and Bouguer’s law Eq. (3.1), it is possible to formulate the directional spectral absorptance and emittance of a glass plate. For hemispherical total values, the integration over the polar angle 0–90° and wavelength spectrum is needed. In the Averaged Net Radiation method developed in [1] for clear and coated glass, the complicated integration is replaced by using special direction-averaged values for spectral reflectivity and penetration angle in a glass plate. The integration over wavelengths is covered by using wavelength bands inside which the radiative properties are quite wavelength-independent.
Figures 3.2 and 3.3 are solved with the method described above. A blackbody is an idealized physical body that absorbs all incident radiation, regardless of wavelength or angle of incidence. A blackbody is also an ideal emitter and its emittance is 1. Figure 3.2 shows the spectral distribution of the blackbody emissive power curve at T=700°C, which is a typical temperature in a tempering furnace.
The area between the curve and the wavelength-axis is equivalent to the total emissive power of a blackbody σT4= 51 kW/m² from which 46% is opaque (λ > 4.5 µm) for glass. The spectral absorptions from that emissive power to clear and low-e coated 4 mm glass are shown in Figure 3.2. One silver layer coating is on the front or back of the glass surface.
The uncoated side of low-e coated glass is more highly absorptive than clear glass when the wavelength is below the opaque band, because the radiation which penetrates through glass thickness is mainly reflected back from the coating on the back surface and then partially absorbed into the glass, or directly absorbed into the coating. Figure 3.2 gives also total values for absorptances, which for clear 4 mm glass is 0.70. Thus, clear 4 mm glass absorbs 70% from the 51 kW/m² above. However, in practice this is not as simple because the surfaces inside a tempering furnace are far from a blackbody.
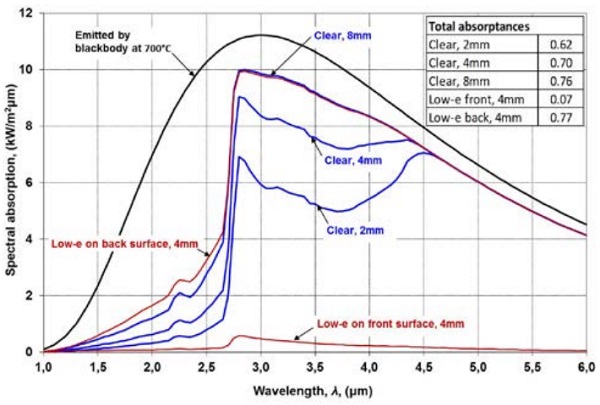
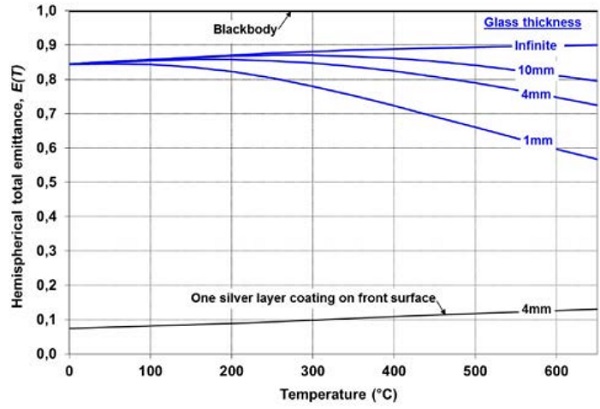
The spectral distribution of the emissive power moves toward shorter wavelengths when the glass temperature increases. Thus, the higher portion of the emission occurs at wavelengths that are transparent for glass, which in Figure 3.3 yields a smaller hemispherical total emittance of clear glass. At infinite thickness and initially also at the biggest thicknesses in Figure 3.3, the emittance increases with temperature. This is due to the increase of glass surface reflectivity at wavelengths above 8 µm.
3.2 Forced convection
Air discharging from a circular orifice forms an axisymmetric jet. Figure 3.4 shows the time-averaged details of a developing turbulent jet. After discharging, the jet starts driving the surrounding air with it and spreading, with decreasing velocity and increasing mass flow. In a tempering furnace, due to relative high blowing distances, the jet temperature when affecting the glass plate is much more dependent on the temperature of the surrounding Tair air than the initial temperature of the discharging flow Tflow.
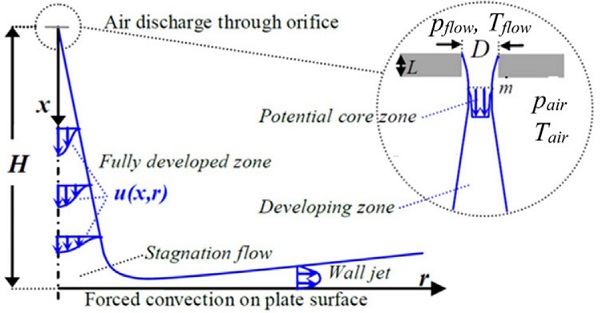
Heat transfer from a single jet to glass surface depends on the blowing pressure (pflow-pair), orifice diameter D, nozzle type, distance between the orifice and glass H, the angle of incidence of a jet to heat transfer surface, and the thermal properties of air. In addition to the influencing factors above, the heat transfer of jet arrays in the tempering furnace depends on the number of blowing holes in a given area and the distances between them. The heat transfer coefficients for different jet arrays can be solved with numerical modelling (CFD), experimentally or from the correlations given by the literature.
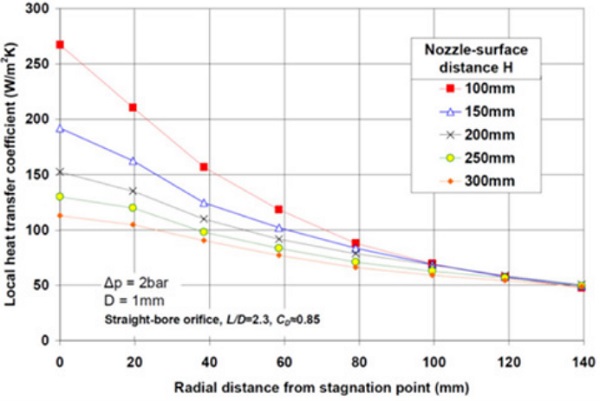
Figure 3.5 shows an example of the measured local heat transfer coefficients at the glass surface under an air jet typical for compressed air convection. In the figure the local heat transfer coefficient near the stagnation point increases strongly when the blowing distance H decreases. When the radial distance from the stagnation point increases, the effect of H on local heat transfer disappears. High local convection rate at stagnation points causes hotter stripes to glass if the blowing distance is too short in relation to the width-wise distance between blowing holes in the tempering furnace.
The evaluation of the correct value of the convection mean heat transfer coefficient h is often difficult, but convective heat flux can be easily specified using it and temperature difference between air and the glass surface qc = h(Tair -Tsurface).
3.3 Contact heat transfer
The bottom surface of the glass and the roller track have a contact line at the distance of the rollers, which is typically between 100 and 150 mm. The heat transfer on the contact area is solid spot conduction between the roller and glass. Outside of the contact area the conduction through a very thin air gap has an effect. The contact heat transfer between a roller and a point at the bottom surface of the glass occurs only during the contact time tct = lct/u, which is a very short period of time.
Next, the contact heat transfer pulse starts after time (Lrp - lct)/u, when the point in the bottom surface off the glass contacts the next roller. The effective contact heat transfer coefficient hct is the average value over the time period Lrp/u, lct is the contact length, Lrp is the roller pitch and u the glass velocity. Heat flux qct with contact heat transfer to the glass is a product between the effective contact heat transfer coefficient and temperature difference between roller surface and glass bottom surface.
In [1] it is given that effective contact heat transfer coefficient between the glass and rollers in a tempering furnace is 1 ≤ hctLrp ≤ 3 W/(mK), which is quite a large range, but in practice it is very difficult to solve for more exact values. Contact heat transfer from the rollers to the glass is a spontaneous phenomenon which cannot be controlled during heating and which does not have much furnace-type-specific variation.
4. Description of the heat transfer problem and its solving method
Figure 4.1 shows a schematic of glass inside a tempering furnace. The glass is exposed to radiation emitted by radiant heaters, rollers and other surfaces inside the furnace. The glass is emitting radiation, and the emission increases when the glass gets hotter. Convection heat transfer between the hot air and glass affects both surfaces. On the lower surface, also contact heat transfer between the glass and rollers takes place.
In order to solve the proportions of radiation and convection heat fluxes to the glass during heating, the glass heating speed must be solved. Thus, the problem is to solve the development of glass thickness-wise temperature profile during heating. The problem is time-dependent, because glass temperature T increases with heating time. The energy equation of glass in Figure 4.1 is

where the first term on the right side stands for conduction. In Eq. (4.1), ρ is density. Specific heat cp and thermal conductivity k of glass depends on temperature. Coordinate x is the perpendicular distance from glass top surface and t is time. Term ∂qr/∂x = S (S is the net radiation source term) takes into account net radiation heat transfer inside the glass.
In actual practise, the temperatures of radiating surfaces and air in furnace are time dependent also because their temperatures decrease when cold glass is loaded into the furnace, until temperatures start to increase back to the set temperatures. The deepness and duration of this drop of temperatures depends on loading degree. Thus, for an all-inclusive model the energy equations for air, rollers and other radiating surfaces in the furnace are also needed, but now it is assumed that their temperatures are constant during heating, which is quite true if the size of the glass moving inside the furnace is small; a 1 x 1 m glass plate oscillating in 2.8 x 6.6 m furnace, for instance.
For solving energy equation 1, the initial and boundary conditions are needed which couple temperatures together. In the upper surface of the glass, radiation and convection are taken into account as

In the lower surface, heat transfer is composed of three components: radiation, convection, and contact heat transfer between the glass and rollers. It can be expressed as

The initial condition is T(x,0) = 20°C. In order to solve Eq. (4.1), the equations for heat fluxes in Eqs. (4.2) and (4.3) are needed.
In Figure 4.1 the radiative heat flux ΣFb(λi,λj,T∞,u)σT∞,u4 hits the upper surface of the glass and ΣFb(λi,λj,T∞,l)σT∞,l4 hits the lower surface. In these glass surfaces the term Fb (λi,λj,T∞) is the fraction of radiative energy of a blackbody between the wavelengths λi and λj at ambient temperature T∞. The emission of glass layer 3 out of the glass ΣFb(λi,λj,T3)σT3 4 increases with increasing temperature T3 of the glass.
In the solution method, the glass is divided into layers (volume elements), the calculation proceeds by time-step ∆t at once and the results after the last time-step are used as initial data for the next time-step. In Figure 4.1 glass thickness (S) is divided into five layers. The thickness of surface layers is one half the thickness of the inner layer. Thus, the thickness step ∆x in glass 1 is S/4.
In the inner layers of the glass, heat transfer occurs by conduction between adjoining layers and absorption of radiation emitted by furnace hot surfaces. Additionally, convection occurs at the surface layer and contact heat transfer occurs in the bottom surface layer.
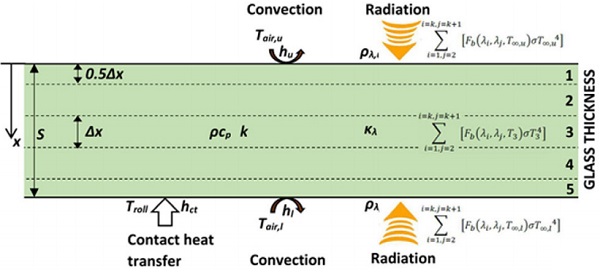
For instance, the energy balance for the lower layer 5 in Figure 4.1 can be written as

where superscript p+1 in glass surface temperature T5 indicates the future after time-step ∆t. The source terms for upperside S5,u and lower-side S5,l radiation for each layer in glass in Figure 4.1 can be formulated in a corresponding way as in [1] for the clear and low-e coated glass. In Eq. (4.1), the term hl(Tair,l-T5) is the convective heat flux qc,l and term hct(Troll-T5) is the contact heat transfer flux qct in Eq. (4.3). The energy balances for the layers 1–4 are formed in a similar way as Eq. (4.4), but without contact heat transfer, and excluding layer 1 also without convection.
5. Results for three furnace models
The Glaston RC series furnace (furnace 1) modelled is equipped with compressed air convection systems on both sides. Top heating resistors in the furnace are open-coil heaters and bottom-heating resistors are open coils covered with a thin metallic cover protecting resistors against broken glass. Top convection of the RC series furnace is divided into separately controllable zones in both length- and width-wise directions with which, based on the information of locations of glass sheets moving inside furnace, the convection rate can be profiled also in the glass moving direction [2B].
Such an invention fully exploits the advantage of compressed air convection technology which is fast and precise controllability. With such a matrix-like control of convection, the blowing to areas without glass can be cut, which decreases the consumption of compressed air. This has a small positive effect on convection rate because the less cold air that is blown into furnace, the less the air temperature drops during heating.
In the first Glaston FC series furnace (furnace 2) modelled the bottom-side compressed air convection system is quite identical to the RC series oven above, but the top side is equipped with a circulating air convection system with elongated nozzle boxes. A nozzle box is divided with a flow-throttling partition into a supply duct and a blowing duct.
Flow-throttling openings present in the partition are positioned to comply with the location and shape of the heating resistances, so that the air flow hits the open coil resistors located in a blowing duct at high speeds [2C]. The purpose of the flow-throttling partition is to minimize the length-wise variation of blowing pressure and boost the air heating. Blowing holes blasting heated convection air against the glass sheet are located at the bottom surface of the blowing ducts.
The third furnace (furnace 3) modelled is formed when compressed air convection on the bottom side of the FC series furnace above is replaced with circulating air convection quite similar to the top side, but the direction of the elongated nozzle boxes is transverse to the glass moving direction.
Thus, the furnaces modelled are the Glaston RC (furnace 1), Glaston FC (furnace 2) and Glaston FC with circulated bottom convection (furnace 3). These furnaces quite comprehensively cover the combinations of compressed-air convection technology and recirculated-air convection technology given in Figure 2.2.
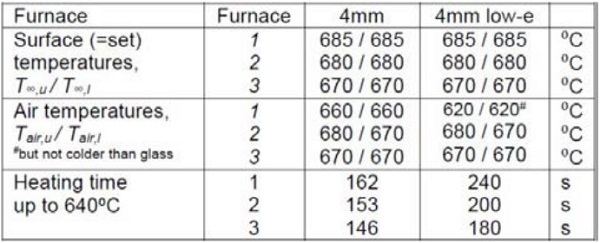
The modelling is done for clear and low-e coated (three silver layer coating) glass with a thickness of 4 mm. Table 5.1 shows the selected circumstances and heating times in the furnaces modelled. The values given, as well as the selection convection set values used in the modelling, are based on actual heating recipes. The convection set values were converted to heat transfer coefficients h on the basis of laboratory measurements and correlations given by the literature [1].
Surface temperatures T∞ used for solving radiative heat fluxes corresponds to the furnaces set temperatures, and surface emissivity values are estimated on the basis of radiative properties literature. The contact mean heat transfer coefficient hct = 15 W/(m²K) is used in modelling the base value, which is given in Chapter 3.3. Roller temperature is Troll = T∞,l. In both furnace 1 and in furnace 2, bottom side air temperature is lower than set temperature due to the reasons given above. Heating times in the Table 5.1 are typical, not minimum, values for the furnaces.
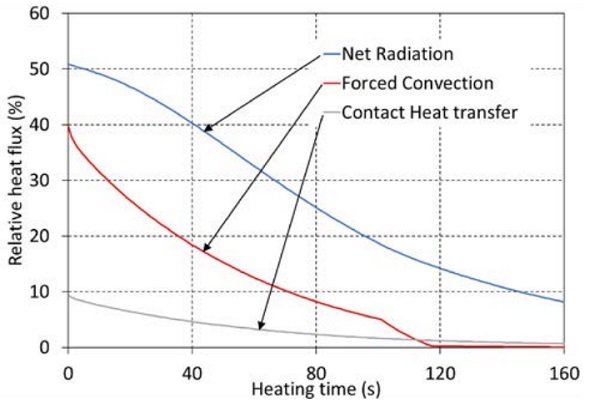
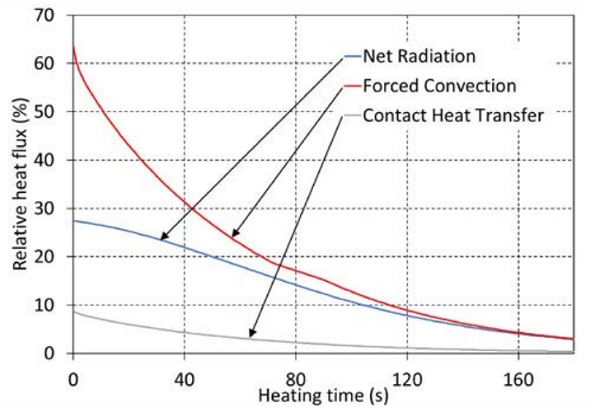
Figures 5.2 and 5.3 show the proportional development of heat flux modes during heating. Figure 5.2 corresponds to the case with the highest portion of radiation, and Figure 5.3 the case with the highest portion of convection. In the figures, convection attenuates clearly faster than net radiation because convection is proportional to temperature difference between the furnace and glass (∆T), but radiation is proportional to the difference between the fourth power of the temperatures ∆(T4).
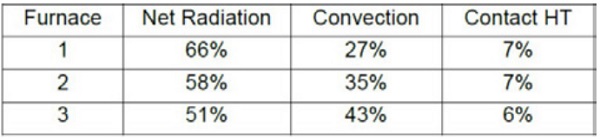
Changes in convection set values during heating can be clearly seen in the shapes of convection curves. In furnace 1 also the absolute value of the radiative heat flux absorbed to clear 4mm glass is highest because of higher set temperature and direct radiation from top side resistors toward to glass.
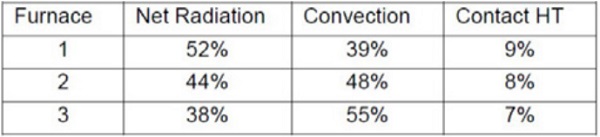
As seen in Table 5.2 the heat is mainly transferred to clear 4mm glass by radiation in all furnaces modelled, even in furnace 3, which belongs to the group of the most convection capable furnaces available. Triple silver layer low-emissivity coating cuts the absorption of the furnace top-side radiation of glass almost totally, but it also cuts the emission via the top-side of glass to the furnace and increases the absorption of bottom-side radiation to glass. Thus, the portions of net radiation to the glass in Table 5.3 are still quite high. In spite of the low-e coating, in furnace 1 radiation is still clearly the main heat transfer mode.
At the beginning of the heating, the portions of convection, which can be seen at time 0 in Figures 5.2 and 5.3, are higher as in Tables 5.2–5.3, but at the end of the heating the portions are lower.
6. Conclusions
Convection, contact heat transfer, as well as about 46% of the radiation in a tempering furnace affect glass surfaces from which heat is conducted deeper into the glass. The rest of the radiation is partly absorbed by glass interior absorptance depending on glass thickness, which slightly decreases the thickness-wise temperature gradient and thermal shock in glass at initial stages of the heating.
In practice, it is about the same is the glass heated more with radiation or convection as long as the glass stays flat during heating, which without effective convection is not possible if the glass top surface is low-e coated. Required top-side convection rate increases with thickness of low-e coated glass, because of increasing absorption of radiation via an uncoated bottom side.
The radiative heat flux hitting cold glass just conveyed in a tempering furnace is quite independent of furnace type, if furnaces set temperatures are the same. The same is true for contact heat transfer from the hot rollers to the glass, which cannot be controlled during heating. The remaining variation depends on where heating resistors are placed and how they are controlled, for instance.
Convection is the most controllable heat transfer mode, which is arranged with external-air or circulated-air convection technologies. Different manufacturers use different designs with differing convection capabilities. That, how reflective and thick low-e coated glass can be heated in a furnace, depends on the maximum efficiency of the top side convection in it. The efficiency of the bottom side convection is only relating to furnace heating speed.
Radiation is the main heat transfer mode for clear glass in all tempering furnaces on the market. The portion of radiation is higher at the end of the heating process compared to at the beginning because convection physically attenuates faster when glass gets hotter. The portion of contact heat transfer from the hot rollers to the glass is between 5 and 10%, increasing with glass thickness-specific heating time. Convection covers, at the highest, 55 to 60% of the heat transferred to low-e coated glass during heating.
References
[1] Rantala, M., Heat Transfer Phenomena in Float Glass Heat Treatment Processes. Tampere University of Technology. Publication, Vuosikerta. 1355, Tampere University of Technology, 2015.
[2] Patents: A=EP1491509, B=EP1737800, C=EP2433912.
[3] Karvinen, R. and Rantala, M., Heat Transfer in Tempering Furnace. Proceedings of Glass Processing Days 1999, Tampere-Finland, p. 52-55.