Article Information
- Digital Object Identifier (DOI): 10.47982/cgc.9. 581
- Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess.
- Published as part of the peer-reviewed Challenging Glass Conference Proceedings, Volume 9, June 2024, 10.47982/cgc.9
- Editors: Christian Louter, Freek Bos & Jan Belis
- This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
- Copyright © 2024 with the author(s)
Author:
- Antti Aronen - Glaston Finland Oy, Finland
Abstract
Optical stress measurement in tempered glass has its challenges. Stresses can be measured optically based on the optical anisotropy behavior of the glass. For example, the stress profile can be measured only offline, or stresses can be measured online at the edge. However, with an online stress calculation in the tempering line based on measured process data, the stress profile can be solved, and more information about tempered glass can thus be obtained. This information about stress level is important for glass processors because it provides information about glass strength and fragmentation which are important values for safety glass that meets the standards.
To solve the residual stresses of tempered glass, it is important to know the glass material and the thermal history of the glass. The thermal history of the glass can be solved based on the information measured from the process and use this data with a heat transfer model. A time-dependent temperature profile is therefore used with thermo-elastic models to solve the stresses. The physical models and the measured data for calculation are presented in this study. The calculation model is then compared to offline stress measurements to find the accuracy of the results. The possible source of errors is also discussed.
1.Introduction
The strength of glass can be increased by tempering, which results in compressive stress in the surface region, and due to equilibrium, a stress profile forms tensile stress in the mid-plane, which affects glass fragmentation. In a tempering process, the glass is heated to above 600 °C, followed by rapid cooling. The heating uniformity and average temperature level have a major influence on stress level and stress uniformity (Aronen & Karvinen 2018). These can be achieved with good control of the heat transfer during the heating part of tempering, in which simultaneous heating with radiation and forced convection is used to balance the heating (Karvinen 1998).
For the stress level, cooling is an important part of the tempering process for achieving the required residual stresses in the glass. To form the residual stress distribution through the glass thickness, the glass is rapidly cooled to less than the glass transition temperature. During the cooling, the temperature difference between the surface and mid-plane is more than 100 °C to obtain tempered glass (Narayanaswamy 1978), and a lower temperature difference to obtain heat-strengthened glass (Aronen & Karvinen 2018). Forced convection must therefore be used for cooling to temper thin glass. However, forced convection is lower for thick glass and is used more to reach the right stress level and balance the cooling (Gardon 1965).
The heat-treated glass needs to meet several different standards for safety, which define the fragmentation or strength of the glass. The fragmentation or strength depends on several different characteristics of the glass, one of which is the stress level in glass. For safety, the fragmentation of heat-treated glass is defined by different standards that must be met. Worldwide, different standards define the limits, e.g., in Europe, EN 12150-1 (2015) for tempered glass and EN 1863-1 (2011) for heat-strengthened glass, and in the US, ANSI Z 97.1 (2015) and ASTM C 1048 (2018). In these standards, the test methods have been defined, which is necessary for following the production quality.
Typically, standards define the test that needs glass breakage to find the safety of the glass (EN 12150-1 (2015); EN 1863-1 (2011); ANSI Z 97.1 (2015)). However, optical stress measurement devices can be used for non-destructive testing. These can be used online or offline, depending on the equipment. A different polarimeter or scattered light polariscope can be used to measure the change of the light in glass and thus provide a result for the stress level (Anton & Aben 2003; Strainoptics 2024). Depending on the equipment's surface stress, the edge stress or stress profile can be measured. This information can be used to follow the stresses in the glass and determine the changes in the stress level. This measurement can be used to find heat-treated glass, which lacks all the safety factors. The glass stress profile or midplane stress is relative to glass fragmentation and can be used to estimate the average fragment size or number of fragments in a defined area (Akeyoshi & Kanai 1965). This stress profile can be measured in different ways, using not only optical but also indirect methods.
The online stress calculation presented in this paper is an indirect stress measurement method, in which heat-treatment process data can be used to calculate an estimate of the stress profile. The method is based on the information about the glass temperature before cooling and the measured process values during cooling. These data are then used with physical models to calculate the stress profile. Instead of using commercial finite-element (FEM) software (Nielsen et al. 2010; Carré & Daudeville 1996), an in-house one-dimensional program for simulating temperature and stress is used(Aronen 2012; Aronen & Karvinen 2017). The one-dimensional program is used to shorten the time calculations take and enable the obtaining of online results from the tempering line.
2. Stress calculation
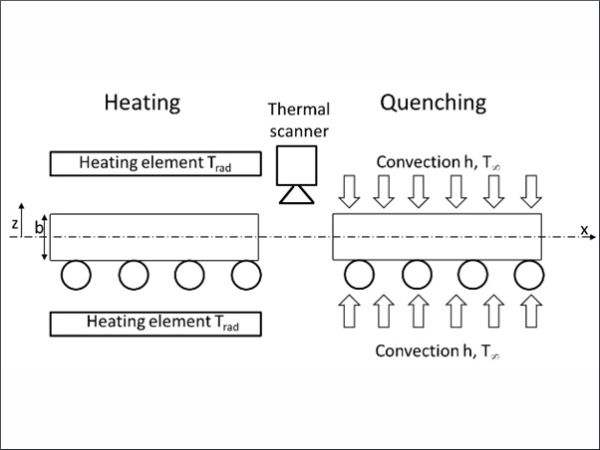
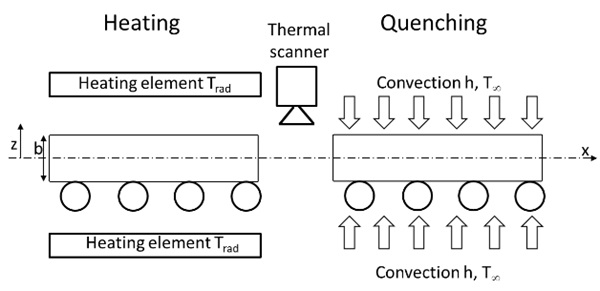
In the tempering process, glass is first heated to above 600 °C. As shown in Fig. 1, the temperature after heating is typically measured from the top or bottom of the glass. The glass then proceeds to cooling, in which residual stresses are formed. In online stress calculation, the idea is to use the glass temperature after heating and measured process data from cooling to solve the transient heat transfer from the glass during the cooling and use the result temperatures to solve the stresses in the glass. The transient heat transfer is well known, and it can be solved effectively with numerical methods(Incropera 1996), when initial and boundary conditions are defined. The theory of the transient heat transfer is discussed further in Chapter 2.1.
The viscoelastic model of glass has been extensively studied in recent decades to obtain a good model to present the mechanical behavior of the glass (Scherer 1986; Narayanaswamy 1971, 1978). This model is used for stress calculation, and a time-dependent temperature history is used as an external load for this solution. The theory of the stress calculation and viscoelastic model is presented in Chapter 2.2.
2.1. Thermal equations
The time-dependent temperature field can be solved with the transient heat transfer equation when the boundary conditions are known. The heat transfer in the solid material is based on the equation

where 𝜌 is the density of the glass, 𝑐𝑝 is the specific heat of the glass, 𝑘 is the thermal conductivity of the glass, 𝑇 is the temperature, 𝑡 is the time, and 𝑧 is the coordinate over the thickness.
To solve this equation, the boundary condition for heat flow from the surfaces 𝑞 needs to be defined as
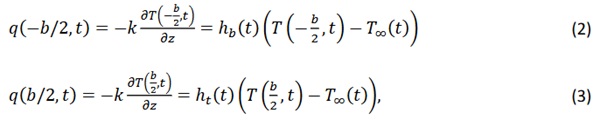
where 𝑏 is the thickness of the glass plate, ℎ𝑏 is the heat transfer coefficient from the bottom surface, and ℎ𝜕 is the heat transfer coefficient from the top surface. Temperature 𝑇∞(𝑡) is the cooling air temperature at different times.
The radiation can also be included in the heat transfer calculation. For the cooling part, radiation has a minor influence on thin glasses because convective cooling plays a dominant role. However, for thicker glasses and heat-strengthened cases, radiation plays an important role. The radiation can be included in transient heat transfer in different ways. Radiation can be included in Eq. 1 with a source term, or radiation can be added in boundary conditions (Eq. 2 and 3), as is typically done with opaque material. The Averaged Net Radiation method (Rantala 2015) has been used as the radiation methodin the paper.
For the boundary condition equation, the average convective heat transfer coefficient ℎ can be calculated with the correlation by Martin (1970),
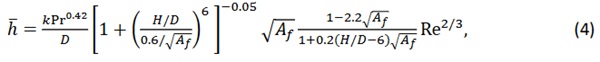
where the limits for the correlation are

In this equation (2), H is the nozzle-to-plate distance, D is the nozzle diameter, Af is the ratio between the nozzle area and free area, Re is Reynold’s number, and Pr is Prandtl’s number. When the nozzle geometry, material properties of air, and pressure at the nozzle are known, the equation can be used to solve the heat transfer coefficient at different times during cooling. The air temperature at different times also needs to be known to solve the time-dependent temperature distribution.
For the numerical solution, either an explicit or implicit solver can be used, where the initial temperature for the solution is the temperature after heating, measured by the thermal scanner. For the solution, the volume needs to be divided into the control volumes, where nodes present the temperature of the whole volume (Fig. 2). The accuracy of the solution and the calculation time depends on the amount of the nodes/control volumes (Aronen 2012).

2.2. Mechanical model
When the history of the temperature distribution, shown above, and the mechanical properties in a viscoelastic material are known, the stress field can be calculated. The theories of thermal stresses, viscoelasticity, and structural relaxation of the glass are shown below and more information about theories can be found e.g., Noda et al. 2003; Scherer 1986; Narayanaswamy 1971, 1978. For viscoelastic material, the material behavior is time-dependent, whereas the behavior is elastic at low temperatures, but the behavior is viscous at high temperatures. The viscoelasticity of the glass can be represented with the Maxwell model, see e.g., Scherer 1986. Because temperature and strain can change as a function of time, the complete time history must be taken into account using hereditary integrals:
![]()
where 𝜀𝜕ℎ is the thermal strain, 𝜎𝑖j is stress, 𝜀̅ and 𝑒𝑖j are strains, K is the bulk modulus, G is the shear modulus, and 𝜉(𝑡) is the reduced time. Because glass is a thermorheologically simple material, the reduced time 𝜉(𝑡) can be used to take the relaxation times at different temperatures into consideration with a shift function and fictive temperature (Narayanaswamy 1971, 1978).
For stress calculation, the physical model is well known. However, the information from material properties is not good. The material properties vary between the references (Nielsen et al. 2010; Carré & Daudeville 1996; Schneider 2004; Aronen 2017). The change in the results depending on the material property changes was previously studied by Aronen & Karvinen (2017), and different material properties have a different influence on the residual stresses. The numerical solution of mechanical model is more discussed by Aronen (2012).
3. Experimental results
The accuracy of the online stress calculation based on the measured process values in the glass tempering process was studied through experimental work. In the test set, 28 glass panes with different thicknesses and sizes were tempered. The process data were collected for each pane, and the results were compared to SCALP measurements (Anton & Aben 2003; GlasStress 2024)
For the stress calculation, the average temperature of the glass was used. It was observed that in all the glass panes, the temperature distribution was relatively uniform (typically within +/- 3 °C) and average temperature presents the whole pane well. In the SCALP measurements, the stresses were measured at the 9 points (center, corners, and the middle of the edges). The average of these results is then used in comparisons with results calculated with process data. Measurements at the edge were done 150 mm from the edge.
The model shown above and presented in more detail in previous studies (Aronen 2012; Aronen & Karvinen 2017) is now used to calculate the stresses for each pane. The average temperature and cooling conditions are used as the initial and boundary conditions for the calculation, and material properties are set to match results. In the temperature and stress calculation the edge effect was not included and stresses in x- and y-directions were same.
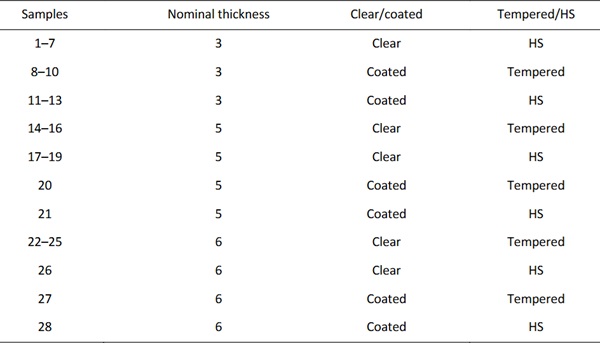
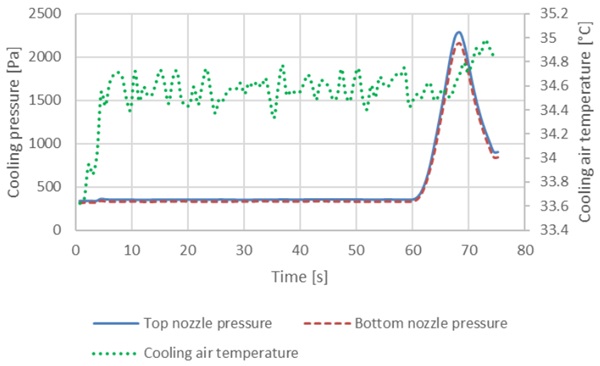
An example is the test set for thicknesses from 3 mm to 6 mm in tempered and heat-strengthened glass. Both clear and low-E coated glasses were tested. The glass thickness and types are listed in Table 1. For example, the collected process data of the cooling pressure and temperature for sample 1 is shown in Figure 3. In sample 1, the glass thickness is 3.15 mm, and the glass temperature before cooling is 645.7 °C. The pressures for the top and bottom are close to each other for clear glass.
Table 1. List of glass thickness and types for samples.
The calculated and measured stresses for all the sample cases are shown in Figs. 4 and 5. The surface stress results are compared in Fig. 4 and the mid-plane stress results are compared in Fig. 5.
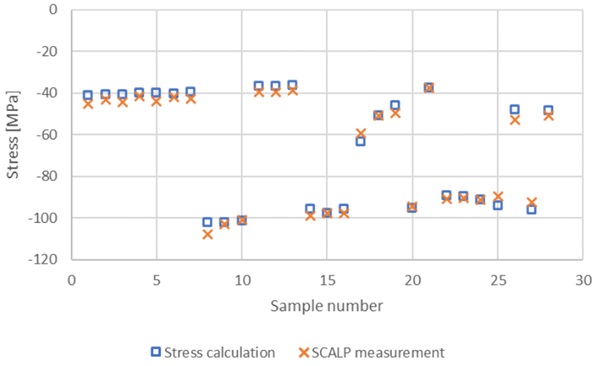
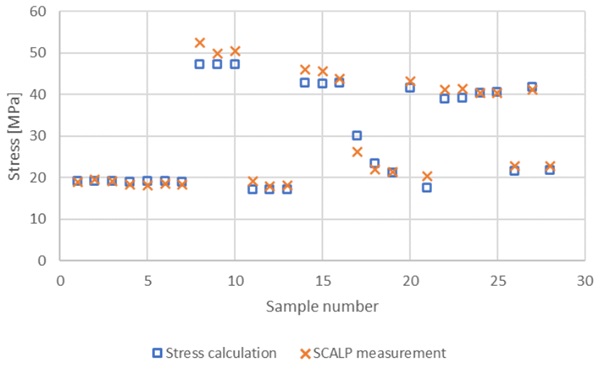
The calculated and measured stresses followed each other well. All the results, except samples 8, 17,and 21 were within 10% when comparing the calculated residual stress results and the average of the SCALP results. In addition, all the stresses are within 6 MPa absolute difference between calculated results and SCALP results. Typically, the calculated stress values are lower than the average SCALP values.
There are several different sources of error in calculation and comparing the calculated results with the SCALP results.
First, the physical calculation model used can be too simple or otherwise does not present the defined case correctly. A viscosity or radiation model can be too simple to highlight an error in the results, or a one-dimensional model used in this case may cause a small error.
Second, material properties can cause an error in calculation. For the soda-lime glass, some references present material properties. However, there are usually differences between references. The measurement of the material properties at high temperatures is difficult and can easily cause errors. The material which is used can also vary between the producers.
Third, the accuracy of the heat transfer coefficient correlation varies, depending on the pressure level, and this influences the. results. This is also connected with the radiation model. With high pressure cooling, the convection has more influence on total cooling, but with low pressure cooling, the effect of radiation increases.
The measured data from the process also has several sources of errors. The glass temperature before cooling is measured on the glass surface. The measurement depends on the accuracy of the thermal scanner/camera, which easily causes errors. For calculation, the initial temperature is approximated as uniform over glass thickness and area. In practice temperature is not uniform over the thickness and area, and this is causing some calculation errors.
n the process data, the measured cooling air pressure and temperature can vary, depending on where the measurements are taken, and how well they present the cooling effect. In equipment is no separate measurement for surface temperature to increase the accuracy for radiation calculation. During cooling, the glass can go through several different cooling zones, and it is important, especially when the glass temperature is above 400 °C, to know in which cooling section the glass is to obtain the correct cooling data for each pane.
Glass thickness can also change. This is common when glass is produced in Europe or North America, for example. Glass thickness has a high impact on the calculated stress results, especially with thin glass. The nominal thickness cannot be used for calculation, but the real thickness can be set or measured, depending on the used system.
The SCALP results also contain sources of errors. The accuracy of the SCALP-05 is given as 5% in the equipment manual (GlasStress 2024). For example, these stress measurement results depend on the place where the measurement is made and the direction of the measurement, which are both related to the optical anisotropy of the glass. In the experimental studies the stresses in one pane were found to vary even ± 5-10 % without having substantial change in the fragment size.
4. Conclusions
As shown in the above results, there are differences in the stresses and SCALP measured stresses calculated by the process data. Some errors come from calculations; some from SCALP measurements. When examining the results, the differences are usually systematic, and both are expected to behave similarly with stress level changes.
Several other factors affect glass bending strength, such as the edge quality, so minor changes in stresses only have a small impact on it. The stresses have a higher impact on fragmentation where the changes in stress level can also be observed in the fragment size (Mognato et al. 2017).
Some improvements could increase accuracy. The stress calculation is currently made with the average temperature of the pane. If the larger panes are divided into smaller areas, the accuracy of the calculation for them can be increased. Material parameters and models require further study.
There is always some error in calculated and measured stress results. However, the stress level of the tempered glasses can be monitored online with process data based stress calculation. The accuracy of the stresses is good for monitoring and determining from the results if there is something wrong in the process, or the results are not otherwise within the limits. This online system also follows all the tempered glasses, and the stress level of the test size panes can be compared with the other panes. Typically, the test size panes are smaller than the other panes in production, which explains why thetemperature of the test size panes is typically higher than the temperature of other tempered panes and easily results in higher fragmentation. The fragmentation test therefore presents only the stress level and safety of the individual glass, not the whole production. An online system is thereforeimportant and has its benefits.
References
Akeyoshi, K., Kanai, E.: Mechanical properties of Tempered Glass. Proceedings of 7th International Congress on Glass, Brussels. Paper #80. (1965).
ANSI Z97.1, American National Standard of Safety Glazing Materials Used in Buildings – Safety Performance Specifications and Methods of Test. ANSI (2015).
Anton, J. Aben, H.: A Compact Scattered Light Polariscope for Residual Stress Measurement in Glass Plates. In: Proceedings of Glass Processing Days 2003, pp. 86–88 (2003).
Aronen, A.: Modelling of deformations and stresses in glass tempering. Dissertation, Tampere University of Technology, Finland (2012). https://urn.fi/URN:ISBN:978-952-15-2816-3
Aronen, A., Karvinen, R. Effect of glass temperature before cooling and cooling rate on residual stresses in tempering. GlassStruct Eng 3, 3–15 (2018). https://doi.org/10.1007/s40940-017-0053-6
ASTM C1048-18: Standard Specification for Heat Treated Flat Glass – Kind HS, Kind FT Coated and Uncoated Glass, ASTM (2018).
Carré, H., Daudeville, L.: Numerical simulation of soda-lime silicate glass tempering. J. Phys. IV 6(1),175–185 (1996). https://doi.org/10.1051/jp4:1996117
EN 12150-1:2015, Glass in Building – Thermally Toughened Soda Lime Silicate Safety Glass – Part 1: Definition and Description, CEN. (2015).
EN 1863-1:2011, Glass in Building –Heat Strengthened Soda Lime Silicate Safety Glass – Part 1: Definition and Description, CEN. (2011).
Martin, H.: Heat and mass transfer between impinging gas jets and solid surfaces. Adv. Heat Tran. (1970). https://doi.org/10.1016/S0065-2717(08)70221-1
Gardon, R.: The tempering of flat glass by forced convection. In: Proceedings VIIth International Congress on Glass, Brussels, Belgium (1965).
GlasStress Ltd: Scattered Light Polariscope SCALP instruction manual Ver. 5.8.2, (2024) Accessed January 20, 2024 (2024).
Incropera, F. P., DeWitt, D. P.: Fundamentals of Heat and Mass Transfer, 4th ed. Wiley, New York (1996).
Karvinen, R.: Adaptation of Tempering Furnaces to Coated Glass. Ind. Ceram. 936, 222–229 (1998).
Mognato, E., Brocca, S., Barbieri, A.: Thermally Processed Glass: Correlation Between Surface Compression, Mechanical and Fragmentation Test. In: Proceedings of Glass Performance Days 2017, pp. 14–20. (2017).
Narayanaswamy, O. S.: A Model of Structural Relaxation in Glass. J. Am. Ceram. Soc. 54(10), 491–498 (1971). https://doi.org/10.1111/j.1151-2916.1971.tb12186.x
Narayanaswamy, O. S.: Stress and Structural Relaxation in Tempered Glass. J. Am. Ceram. Soc. 61(3–4), 146–152 (1978). https://doi.org/10.1111/j.1151-2916.1978.tb09259.x
Nielsen, J. H., Olesen, J. F., Poulsen, P. N., Stang, H.: Finite element implementation of a glass tempering model in three dimensions. Comput. Struct. 88, 963–972 (2010). https://doi.org/10.1016/j.compstruc.2010.05.004
Noda, N., Hetnarski, R. B., Tanigawa, Y.: Thermal Stresses, 2nd ed. Taylor & Francis, New York, USA (2003).
Rantala, M.: Heat Transfer Phenomena in Float Glass Heat Treatment Processes. Dissertation, Tampere University of Technology, Finland (2015). https://urn.fi/URN:ISBN:978-952-15-3692-2
Scherer, G.: Relaxation in Glass and Composites. John Wiley & Sons, Inc., USA (1986).
Schneider, J.: Glass Strength in the Borehole Area of Annealed Float Glass and Tempered Float Glass. Int. J. Form. Process. 7(49), 523–541 (2004).
Strainoptics: GASP polarimeter https://www.strainoptics.com/gasp-surface-polarimeter/ (2024). Accessed January 20, 2024 (2024).