Structural Damping of Glazed Facades and Resulting Risk of Vibration under Along Wind Excitations

Article Information

• Digital Object Identifier (DOI): 10.47982/cgc.9.579
• Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess.
• Published as part of the peer-reviewed Challenging Glass Conference Proceedings, Volume 9, June 2024, 10.47982/cgc.9
• Editors: Christian Louter, Freek Bos & Jan Belis
• This work is licensed under a Creative Commons Attribution 4.0 International ( CC BY 4.0) license.
• Copyright © 2024 with the author(s)

Authors:

• Guido Lori - Permasteelisa Group
• Giampiero Manara - Permasteelisa Group

Abstract

The authors investigate the dynamic factor dependency on the major wind excitation parameters, including mean wind velocity, turbulence factor and system dynamic properties, using the Single Degree of Freedom (SDOF) simplification. The reason of the research is the controversial limit stated in the EN1991-1-4:2005, set to 5Hz, which represents the minimum value of the system first natural frequency allowing to ignore dynamic amplification factors to incorporate into the equivalent static approach. While the largest part of the scientific community aims at reducing this value, to avoid additional useless reinforcements and checks, other researchers have identified testing conditions for which vibrations occurred even for natural frequencies up to 14Hz. The authors start from the analysis undertaken in their previous work, identifying damping as the decisive parameter. Differently from what is reported in several literature studies, working conditions of glazed façades often result in inequivalent structural damping larger than the minimum values assumed in numerical calculations. Other experimental data will show that an indiscriminate reduction of the 5Hz limit would probably be unsafe. Recommendations will be given in order to run specific experimental investigations to solve the inconsistent literature experiences and to address the limit in future standards in dependency on specific combinations of wind and system dynamic properties.

1. Introduction

Wind is the major action exciting the façade and regardless of its dynamic nature, it is widely accepted an equivalent static approach for its analysis, like for instance shown in the EN1991-1-4:2005. Resonance effects are taken in account by means of a structural factor cccd, which multiplies the design pressure assessed by the general approach. The structural factor is formed by the product of two functions, one is the size factor cc, which takes in account the effects of non-simultaneous peaks occurring on the overall loaded surface, while the second is the dynamic factor cd, considering the effects of the vibration on the structure due to the turbulence.

A sentence in the Eurocode has always created debates, when design of façade and roof elements is concerned, stating that for façade and roof elements having a natural frequency greater than 5Hz, the value of cccd may be taken as 1. The sentence did not receive general consensus from the scientific community (Geurts et al. 2004) and it is more a source of confusion than an opportunity to make order in a quite complex scenario. Even less clear is what a designer in the United States should consider for dynamic effects on facades, as ASCE7-10:2010 introduces a general limit of 1Hz for the critical natural frequency of structures. In this scenario, Allen et al. 1974 reported that metal and glazing cladding natural frequencies are in the range between 5 and 50Hz, so several times higher than significant wind turbulences. Nagakami 2003 analysed glazing cases with natural frequency ranging from  3.6Hz to 21.8Hz and mean velocity between 17m/s and 30m/s. For the higher velocity and the smallest frequency, around 10% of difference appears in the dynamic response with respect to the static response. 

Experimental tests conducted during the last years (Moravej et al. 2014) have shown that the relatively small scale elements, like PV systems, can be subjected to significant wind induced vibrations even if characterized by much higher natural frequency than 1 HZ ASCE7 limit, like 13Hz in the specific test. In extreme synthesis, it can be said that most part of the researchers and façade engineers believe that the 5Hz limit stated by the Eurocode is too large (Lagasse 2017), but at the same time other researchers experienced unexpected vibrations for systems with larger natural frequency than 5Hz. Apparently they are incompatible conclusions, but the authors would like to give their contribution for a clarification in order to justify the occurrence of so different experiences and to propose guidelines for an efficient analysis of the dynamic effects excited by wind gusts on façade elements. In the following paragraphs, the authors will describe the approach of the Eurocode and will summarize their precedent works on the estimation of the dynamic factor by means of a numerical methodology. Then, novel contents will be presented, starting from an example of experimental results, carried out by the authors in collaboration with the Wall of Wind laboratory, which will show how an indiscriminate reduction of the 5Hz limit could be a critical source of unsafe design. Other experimental results collected by the authors during a campaign on impact loading tests will be used to demonstrate that probably the adoption of more realistic damping factors could justify a relaxation of the 5Hz limit. However, the boundary conditions for the adoption of these relatively large values of damping should be systematically proved and clearly defined for the different types of applications.

A comparative analysis between outcomes of the code approach and the results of the method proposed by the authors is presented, looking for the impact of several factors on the dynamic amplification. Finally, a proposal for future revisions of the Eurocode is discussed, with the scope to make a more comprehensive guide to the designers, which will also resolve and explain the contradictions and the inconsistencies of the current statement. This proposal is not just a way to finalise a divisive subject, but also an opportunity to enhance the focus on the façade, not anymore just an appendage on the building, but as a fundamental element which can contribute to the dynamic building behaviour. Indeed, experimental evidences exist that facades have an impact on the building dynamics. Envelopes give a certain contribution to the damping ratio of the building, comparing measurements conducted before and after the façade installation (Meyyappa et al. 1980; Moore 2016) and more and more studies are conducted about the effect of the façade likewise a Tuned Mass Damper (TMD). Probably, equivalent static approach will need to be upgraded in future years, in order to take in account not just dynamic effects on the façade, but also the dynamic interactions between façade and building.

2. EN1991-1-4:2005 content

The structural factor is defined in the Eurocode by the following formulation:

The structural factor can be seen like the product of two terms, the size factor cs, which takes in account the effect of non-simultaneous occurrence of peak wind pressure on the surface:

And the dynamic factor cD, which accounts for the vibration of the structure under the wind turbulence:

Table 1: Description of the terms for the structural factor calculation according to Eurocode EN1991-1-4:2005, Annex B.

The Table 1 shows the different descriptions of three elements of the full formulation, the peak factor, the background factor and the resonance response factor, in function of the zS, the reference height and Iv(zs), the turbulence intensity:

The code contains two different methods for the calculation of the structural factors (Steenbergen 2012), the method 1 (Solari 1982; CNR 2010) explained in Annex B and the method 2 (Drybye and Hansen 1999) explained in Annex C. The Table 1 shows in detail the method 1.

3. Previous work of the authors

The authors have developed a methodology to verify the approach of the Eurocode by an analysis in frequency domain (Lori et al. 2022). In particular, they focused on the dynamic factor. They have generated different Power Spectral Density of the wind, as explained in Fig.1. In the formulation, z is the height of the system, vm is the mean wind velocity and σV is the standard deviation of the turbulent wind.

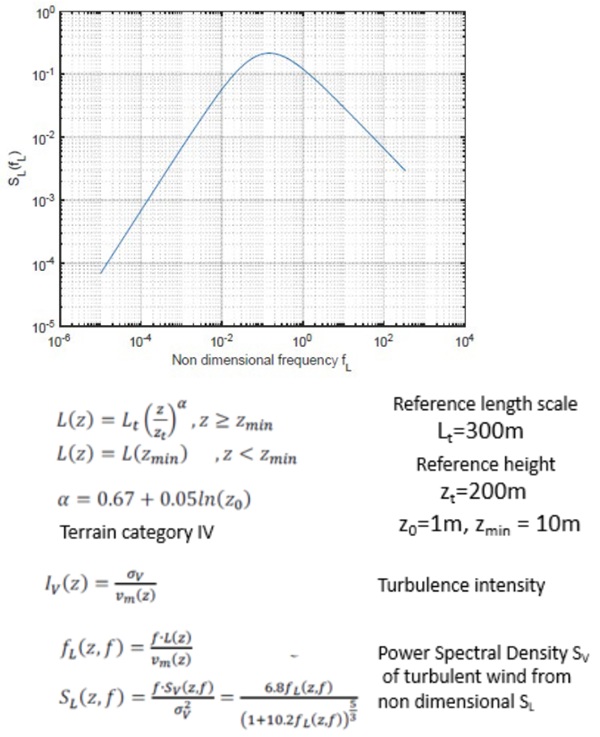
Then, from the PSD SL they have generated a large number of wind velocity time histories, reconstructing them by the Monte-Carlo method:

The pressure time history is derived by (5) by means of the velocity time history:

Then, by an operation of Power Spectral Density, the PSD SP(ω) of the pressure is obtained.

The modelling of the system has been conducted by the Single Degree of Freedom (SDOF) representation (Biggs 1964), with the advantage to reduce to three the number of parameters required to describe all the possible different systems. Once a certain degree of damping ratio and a mass have been defined, a family of systems with different natural frequency have been generated, by varying the system stiffness and obtaining a sequence of frequency response functions H(ω). So, multiplying the input SP(ω) PSD of the pressure by the H(ω), a SD(ω) PSD of the output in terms of displacement has been obtained for each of these systems and for each different type of wind velocity properties, like shown in Fig.2. 

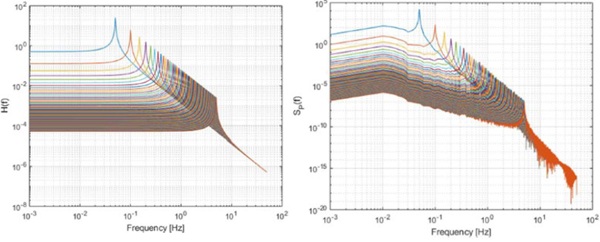
The proposed dynamic factor is given in this way by the ratio between the dynamic response and the quasi-static response. For simplicity a peak factor 3.5 has been considered regardless of the shape of the response PSD SD(ω). As a consequence, the proposed approach is conservative for low natural frequencies and non-conservative for high natural frequencies. The proposed dynamic factor is expressed by:

Where the dynamic and the quasi-static displacements are given by:

And the standard deviations of the wind pressure and of the dynamic response are given by:

An applicative example has been run to compare the proposed methodology with the outcomes given by the method 1 of the Eurocode. The exercise, presented initially in (Lori and Manara, 2022) has been integrated with more results, in particular given by direct integration methods.

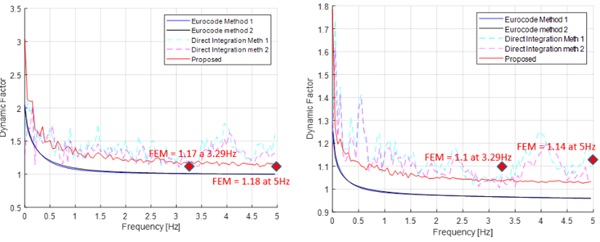
A monolithic glass of dimensions 3x6m has been loaded by an experimental pressure measurement (measured on site in London during the September 2019, Fig.3) and solved by the finite element commercial code Straus® and by two different algorithms of numerical direct integration, implemented into a procedure developed in Matlab®. The proposed methodology and the Eurocode method have been applied by deriving the mean wind velocity, the turbulent length scale and turbulent factor from the measured pressure time history. The thickness of the glass has been varied keeping the same total mass, by means of a fictitious density. In this way the natural frequency of the system has been changed in the range 0.036-8Hz. Larger frequency would have been of interest, but it has been decided to limit the largest frequency to 8Hz, because the sampling frequency of the pressure signal was of 20Hz. Three damping ratio values has been adopted in the sensitivity analysis:  0.1%, 1% and 5%. The dynamic factor from the numerical simulations is calculated by its definition, so by the ratio between the maximum displacement by dynamic analysis and the maximum displacement under quasi static analysis.

One extract of the results is shown in Fig.4: the dynamic factor estimated by the EN1991-1-4 approach appears in general lower than estimated by the other methods, while there is a certain consistency between FEM approach, direct integration methods and proposed approach. In particular, it seems that the difference between the code approach and the other tested method increases for larger damping ratios. In conclusion, it can be said that the EN1991-1 -4 method is not fully consistent with the outcomes of numerical calculations for the estimation of the dynamic factor.

4. Experimental evidences about inputs of the dynamic factor calculation

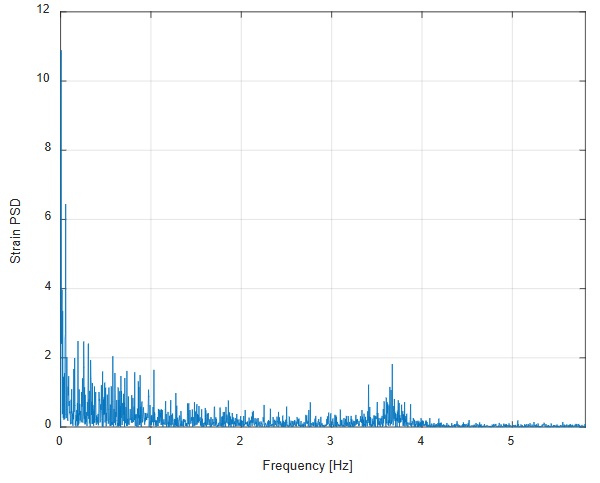
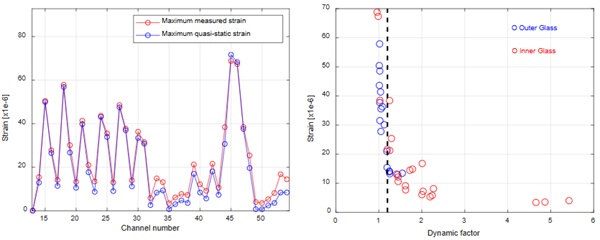
Analysing the proposed methodology results in comparison with the outcomes of the Eurocode method, the authors search for explanations of the differences, by means of investigations about the parameters that influence in major way the method outputs. In test conducted by the authors in collaboration with the Wall of Wind testing facility (Alawode et al. 2023), the Power Spectral Density of the strain on a glazing shows around 30% of the spectral area concentrated around the first natural frequency of the experimental model, at around 3.8Hz. When the statistical analysis of the measured time history is undertaken, it is noticed that peak factor is around 5. The specified test has been run in order to study the wind induced vibrations and wind driven rain of single skin façade with and without architectural  fins. For the scopes of this paper, the correlations between the strain time histories measured in different positions of outer and inner glass of the double glazing unit and the expected quasi static behaviour are investigated. As anticipated, several strain gauges are characterized by Power Spectral Density of the strain measurement with a peak at around 3.8Hz, as shown in Fig.6.

In addition to the strain gauge sensors, also pressure sensors have been used and positioned on the polycarbonate side of the model. In particular, 110 pressure sensors have been distributed on the surface. In Fig.7 at the left side, the comparison between the maximum strain of each channel of the strain gauge sensors (3 channels per each sensor, measuring strain at 0, 90 and 45 degrees) and the expected quasi-static strain is shown. The expected quasi static strain has been calculated by multiplying the peak of the average pressure over the 110 sensors for the ratio between the mean value of the strain channel along the time history and the mean value of the average pressure along the same duration of the measurement. The right side shows on the contrary the correlation between the dynamic factor of the channel (ratio between the two values reported in the left figure) and the maximum strain value. When the dynamic factor exceeds the 1.2 value (dashed black line), the dynamic effect can’t be neglected. By this example, it can be seen like a significant vibration is occurring, although the resonance of the system is at 3.8Hz, a frequency that many researchers considers large enough to ignore dynamic effects. Analysing the correlation of Fig.7, it should be said that the strain measurements with the largest dynamic factors can be ignored, because characterized by small values of strain. However, dynamic factors in the range [1.2-2] are corresponding to strain peaks of a relevant magnitude. 

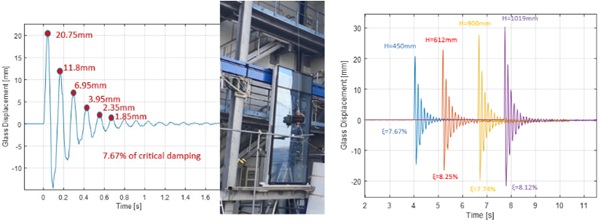
It is easy to check how the damping factor has a fundamental effect on the dynamic factor. Based on literature studies about the behaviour of glazing on different supports, it should be expected adamping in the range of 1% of the critical damping (Lenk et al. 2010), as also recommended in EN1991-1-4 . However, when glazing panels under representative supporting details of the site conditions are tested, significantly larger values of damping are measured. For instance, in Fig. 8, time histories of displacement recorded during impact testing in Permasteelisa Test & Lab have shown like values of 7-8% of critical damping are common.

Another important parameter which has a major impact on the estimation of the dynamic factor is the peak factor. Comparing the definition of the EN1991-1-4 with the distribution of the peak factor obtained by the proposed method, it can be seen like the Eurocode seems to underestimate the factor, in particular because of an underestimation of the upcrossing frequency (Fig.9). 

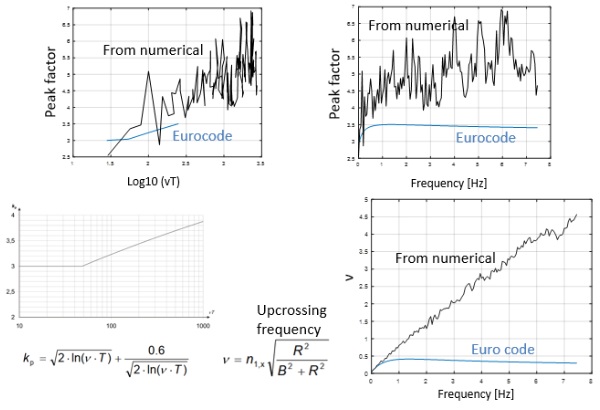
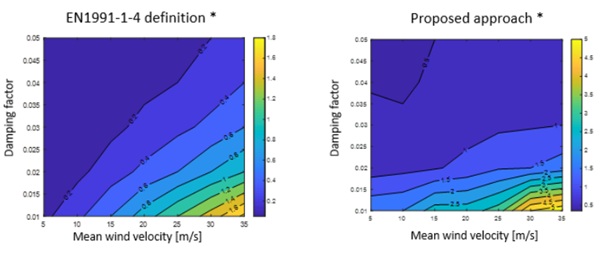
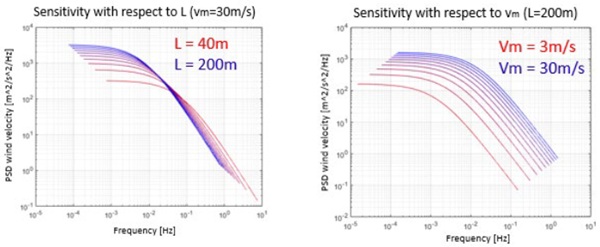
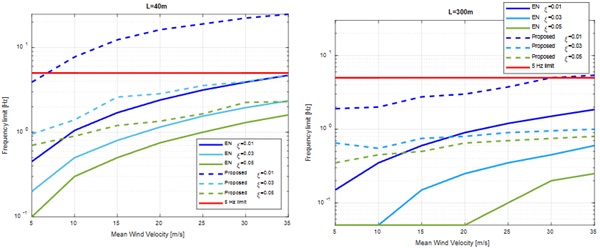
Making sensitivity analysis on the EN1991-1-4 definition it seems like the worst case scenario of the code frequency limit (5Hz), refers to a condition of low damping for high mean wind velocity (35m/s) and small turbulent scale (40m, H=10m), as it can be seen in Fig. 10, where the frequency limit is calculated searching for the dynamic factor 1.2 (Borri et al. 2007). However, according to the method proposed by the authors, under these conditions the code seems non conservative, and it could be the reason of the literature studies that contradict the statement. For applications with larger turbulent scale (L=300m, Fig. 10), consistent with applications on high rise buildings, the frequency limit of the code would be significantly smaller. The method proposed by the authors confirm this conclusion, excluding zones with small damping where 5Hz seems still appropriate. The sensitivity of the PSD wind velocity in function of the turbulent scale (Fig.12), shows how the smaller L is more critical for the major energy content at higher frequency.

5. Proposal for further code revisions

The frequency limit, stated as 5Hz in the current version of the EN1991-1-4, should be probably defined in function of the parameters with the major influence, like turbulent length scale, mean wind and damping ratio as shown in Fig.13. The current definition seems non conservative for small turbulent scale and low damping, while it could be probably reduced for large part of the applicative cases. For instance, when the 40m of turbulent length scale is concerned (left chart of Fig.13), the Eurocode would give the current 5Hz limit for the largest mean wind velocity and for a damping factor 0.01. According to the method proposed by the authors, the same limit could be reasonable only when larger damping factor are assumed, in the range of 3%. For turbulent scale lengths of one order of magnitude more, the Eurocode would supply a limit of around 2Hz assuming the damping factor 0.01, while the method proposed by the authors define a 1Hz limit for damping factor 0.03. So, it seems illogical to aim at defining a unique limit for all the applications, while it would be more effective to allow the designer to search for the critical frequency in function of the parameters shown in Fig. 13.

6. Conclusions and future work

The 5 Hz limit stated in the Eurocode EN1991-1-4 for ignoring resonances of systems under along wind excitations has been always debated: for most part of the applications it seems conservative, but several studies in literature exist that show dynamic effects at large frequencies. The authors have investigated the problem by an approach based on SDOF, PSD of wind excitation and reconstruction of possible excitation wind pressure time histories. By the obtained results, it appears that the Eurocode approach is not on the safe side under certain conditions and this could explain the controversial literature experiences. The damping factor seems the parameter that governs the phenomenon and the authors invite the researchers to investigate in detail the behaviour of façade elements under serviceability conditions, as probably today the recommended damping values are underestimated. By adopting realistic damping factors, probably the risk of vibrations will be significantly reduced and identified for a few applicative scenarios.

References

Alawode, J.K., Vutukuru, K.S., Elawady, A., Lee, S.J., Chowdhury, A.G., Lori, G., Wind-Induced Vibration and Wind-Driven Rain Performance of a full scale single-skin façade unit with vertical protrusions, Journal Architectural  Engineering, 29(2), 2023, DOI: 10.1061/JAEIED.AEENG-1393.
ASCE/SEI 7-10, Minimum Design Loads for Buildings and Other Structures, 2010
Allen, D.E, Dalgliesh, W.A., Dynamic Wind Loads and Cladding Design, NRC Publication Archive, 1974
Borri, C., Pastò., S., Lezioni di Ingegneria del Vento, 2007.
Biggs, J.M., Introduction to structural dynamics, McGraw-Hill Book Company, New York, 1964
Dyrbye, C., Hansen, S.O., Wind Loads on Structures. John Wiley & Sons, New York, 1999
Geurts, C.P.W., Van  Staaiduinen, P.C., De Wit, M.S., Towards a reliable design of façade and roof elements against wind loading, TNO Building And Construction Research, Delft, The Netherlands, Heron Vol.49, No.2, 2004
European Committee for Standardization (CEN), 2005, EN1991-1-4, Eurocode 1: Actions on structures, Part 1-4 General Actions-Wind Actions
La Gasse, L.C., Structural Reliability Assessment of buildings subjected to wind loadings. An assessment of the main bearing structure at foundation level of dynamically sensitive buildings designed within the Eurocode Framework, Master  Science in Civil Engineering Thesis, University of Delft, 2017
Lenk, P., Coult, G., Damping of Glass Structures and Components, Challenging Glass 2 – Conference on Architectural and Structural Application on Glass. Bos, Louter, Veer. TU Delft, 2010
Lori, G., Manara, G., A numerical assessment to estimate the dynamic factor for wind excited façade elements having a natural frequency smaller than 5Hz, IN-VENTO 2022-17th Conference on Wind Engineering-Polytechnic University of Milan, 2022
Meyyappa, M., Palsson, H., Craig., J.I., Modal parameter estimation for high rise building using ambient response data taken during construction. In G.C. Hart editor Dynamic Response of Structures, experimentation, observation, prediction and control. Pages 141-150. ASCE, NY, USA, 1980
Moore, A.J., Dynamic characteristics and wind induced response of a tall building, PhD Thesis, 2016
Moravej, M., Chowdhury, A., Irwin, P., Zisis, J., Bitusmalak, G., Dynamic Effects on Wind Loading on Photovoltaic Systems, ICWE14, 2014
Nagakamy, L., Probabilistic Dynamics of Wind Excitation on Glass Façade. Dissertation of Master Degree, Darmstadt. 
National Council Research of Italy, Guide for Assessment of wind actions and effects on structures, CNR-DT 207/2008, Rime 2010 
Solari, G., Alowing wind response estimation: closed form solution. ASCE Journal of the Structural Division, 108 (1): 225-244, 1982
Steenbergen, R.D.J.M., Vrouwendenvelder, A.C.W.M., Geurts, C.P.W., The use of Eurocode EN1991-1-  4 procedures 1 and 2 for building dynamics, a comparative study. Journal of Wind Engineering and Industrial Aerodynamics, 107-108, 299-306, 2012