Collaborative Optimized Design of Glazing Parameters and PCM Utilization for Energy-Efficient Glass Curtain Wall Buildings

Authors: Xinrui Zheng, Yan Liang, Haibin Yang, Yingyan Zeng and Hongzhi Cui

Key Laboratory for Resilient Infrastructures of Coastal Cities (MOE), College of Civil and Transportation Engineering, Shenzhen University, Shenzhen 518060, China

Source: Buildings 2024, 14(1), 256; MDPI

DOI: https://doi.org/10.3390/buildings14010256

(This article belongs to the Special Issue Energy Efficiency and Sustainability in Construction and Building Materials)

Abstract

Glass curtain walls (GCWs) have become prevalent in office buildings, owing to their lightweight and modular characteristics. However, their lower thermal resistance, compared to opaque walls, results in increased energy consumption. Incorporating phase-change materials (PCMs) provides a viable solution through which to address the susceptibility of GCWs to external conditions, thus enhancing thermal performance and mitigating energy concerns. This study delves into the influences of the glazing solar heat gain coefficient (SHGC), the glazing heat transfer coefficient (U-value), and PCM thickness on the energy performance of buildings. Using Design Builder (DB) software version 6.1.0.006, a multi-story office building was simulated in different climatic zones in China, covering the climatic characteristics of severe cold, cold, hot summer and warm winter, cold summer and winter, and mild regions. The simulation results quantitatively elucidated the effects of the glazing parameters and the number of PCMs on thermal regulation and energy consumption. A sensitivity analysis identified the glazing SHGC as the most influential factor in energy consumption. Additionally, by employing Response Surface Methodology (RSM), the researchers aimed to achieve a balance between minimal building energy consumption and economic cost, ultimately determining an optimal design solution. The results demonstrated significant energy savings, ranging from 20.16% to 81.18%, accompanied by economic savings, ranging from 15.78% to 79.54%, across distinct climate zones in China.

1. Introduction

In recent decades, glass curtain wall (GCW) buildings have been widely constructed in cities, due to the increasing demand for architectural aesthetics and the rapid development of lightweight and prefabricated construction. However, compared to conventional wall-based buildings, the lower thermal resistance of the glazing system makes the building more vulnerable to outdoor environmental conditions [1]. As a result, GCW buildings have negative impacts on the energy demand for indoor thermal comfort. To address this issue, it is essential to rationalize the performance of architectural glazing [2,3]. Additionally, phase-change materials (PCMs), with high heat storage density and isothermal phase-change properties, offer a solution for regulating indoor temperature and reducing building energy consumption [4,5]. Therefore, integrating the design of architectural glass performance with the incorporation of PCMs in GCW buildings is anticipated to significantly decrease overall building energy consumption.

Optimizing GCW design by adjusting parameters such as the solar heat gain coefficient (SHGC) and the heat transfer coefficient (U-value) is critical to achieving energy savings. Previous studies have examined the impacts of multiple design parameters of windows on building energy efficiency [6,7,8,9]. For example, Lantonio et al. [10] found that optimal glazed window design can result in energy savings, ranging from 11% to 18%, by simultaneously optimizing the window’s U-value, SHGC, visible transmittance, and window-to-wall ratio (WWR). Lam et al. [11] also identified the WWR and the SHGC as the most significant parameters affecting end-use energy consumption in cold climates. Moreover, Feng et al. [12] investigated the effects of the U-value and the SHGC on building energy consumption in cold climates, determining that the U-value for outer windows should be 0.780 W/m²-K, and the SHGC should not be lower than 0.474. Furthermore, Liu et al. [13] found that the SHGC is the most influential variable in regions with high cooling load demand. In practical applications, one effective approach to modifying glass properties involves the application of solar control window film (SCWF) [14]. According to the International Window Film Association, standard clear glass typically reflects about 6% of solar radiation, absorbs 5%, and transmits the remaining amount [15]. The use of SCWF enables precise control over these reflection and absorption values. Moreover, empirical studies have demonstrated that the utilization of SCWF can significantly reduce the energy consumption associated with heating and cooling systems [16]. This underscores the notable potential impact of SCWF in optimizing energy efficiency.

PCMs have been identified as a potential solution through which to regulate indoor temperature in buildings [17,18]. However, the effectiveness of integrating PCMs into the building envelope is influenced by various factors, including the layer structure and properties of the PCM [19,20,21]. For instance, Mohseni et al. [22] investigated the impacts of the phase change temperature, thickness, and position of a PCM on building energy consumption in Australia, and found that a PCM with a phase change temperature of 21 °C and a thickness of 10 mm, applied on roofs and walls, provided the optimal energy consumption. Kishore et al. [23] found that the phase change temperature of a PCM was the most influential parameter for building heat gain. Nevertheless, phase change temperature is not the only parameter to consider when selecting PCMs [24]. These findings indicate that the effects of different PCM parameters on building energy efficiency are not universal.

Research on integrating PCMs in building envelopes has been also conducted in various regions with different climatic conditions. Qu et al. [25] studied the influences of four key parameters of PCMs on the energy consumption and indoor temperature of buildings for six climate zones in China. They found that different regions are suitable for different combinations of PCM parameters. For Pakistani climates, a PCM with a melting temperature of 24 °C and a thickness of 40 mm was found to be the best choice when placed on the inner side of the building envelope [26]. In subtropical climates, PCMs are best positioned on the inner surface [27], while the external positioning of PCMs was found to be more energy efficient in Tunisian climates [28]. These studies show that the effectiveness of integrating PCMs into building envelopes varies by region and is affected by various factors, such as PCM parameters and location.

Additionally, the application of PCMs in glazing systems has been widely studied [29,30,31,32,33,34,35,36]. For instance, Zhong et al. [37] conducted research on the impacts of the thermophysical parameters of PCMs on the dynamic heat transfer of PCM-filled glass windows. The simulated results concluded that the thermal insulation and load-shifting effects of PCM-filled glass windows, enhanced with the increasing fusion latent heat of the PCM. Silva et al. [38] found that maximum indoor temperature of a PCM window shutter could be reduced by 8.7% during the daytime, and the minimum indoor temperature increased by 16.7% at night compared to common window shutters. Li et al. [39] studied the effects of PCM melting temperatures, PCM layer thicknesses, and glazed roof slopes on the energy consumption and indoor thermal environment of a PCM-filled glazed roof. The findings revealed that the energy savings of a glass roof filled with PCMs can be as high as 47.5%, and increasing the PCM melting temperature and PCM layer thickness can effectively reduce indoor temperature. Overall, it can be inferred that applying PCMs in GCW buildings will have synergistic effects on reducing energy savings.

While numerous studies have explored the integration of PCMs with glazing systems, there is a notable dearth of research focusing on internal partitions. In this study, the researchers address this gap by examining the impacts of key parameters, specifically, the SHGC, U-value, and PCM thickness, on the thermal performance of GCW buildings. By conducting parameter optimization, using Response Surface Methodology (RSM), the authors aimed to unveil the relationships between glazing parameters and PCM thickness, while minimizing building energy consumption. This research significantly contributes to the field of PCM applications in the context of GCW buildings, laying the groundwork for advancements in the design, the optimization of glazing parameters, and the effective utilization of PCMs.

2. Methodology

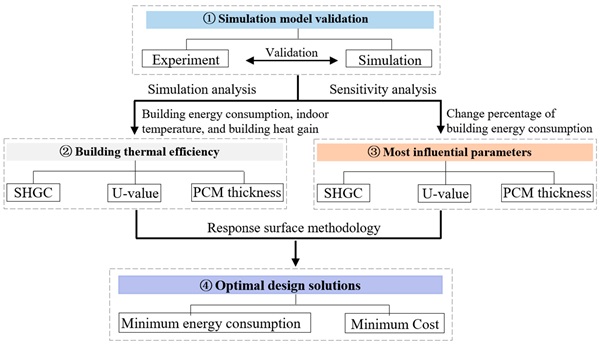
In this study, the effects of PCM application on GCW buildings are investigated, and their design is optimized through a four-step methodology, as illustrated in Figure 1. Firstly, small-scale room models were constructed, both in the laboratory and with the Design Builder (DB) software. The experimental results and simulations were then compared to validate the accuracy of large-scale GCW building models. Secondly, numerical methods were used to investigate the effects of three key parameters, namely the SHGC, U-value, and PCM thickness, on the energy consumption, indoor temperature, and building heat gain of GCW buildings in five different climate zones in China. Thirdly, a sensitivity analysis was performed to identify the most influential parameters affecting the energy consumption in each climate zone. Finally, the RSM was employed to develop an optimization model based on the thermal energy consumption of the three variables (SHGC, U-value, and PCM thickness) to determine the optimal design parameters.

2.1. Experimental Study

As depicted in Figure 2, a set of four laboratory room models (480 mm × 480 mm × 490 mm) was assembled. The first model served as a blank control group, constructed with a 5 cm thermal insulation board. Type K thermocouples with a resolution of ±1.1 °C/0.4% were meticulously positioned at the center of the model, and temperature profiles were recorded using a multi-channel data recorder (TP700, Shenzhen TOPRIE Electronics Co., Ltd., Shenzhen, China). The second model involved applying SCWF on the glass to investigate the impact of solar heat gain on the indoor temperature. The bluish-colored SCWF was chosen for its abilities to absorb sunlight, mitigate heat, and effectively filter both ultraviolet and visible light. Figure 3 presents the spectral characteristics of glass with and without SCWF, including solar transmittance and solar reflectance values in ultraviolet, visible, and near-infrared light. Furthermore, the thermal conductivity of SCWF glass was measured to be 0.94 W/(m-K) at 26 °C, with an accuracy within ±3%, using the transient hot wire method (TC3000S, XIATECH Co., Ltd., Xi’an, China). The third model utilized iron boxes (119 mm × 172 mm × 19 mm) filled with PCMs affixed to the inner walls to investigate the influences of PCMs on the indoor temperatures in buildings. The PCM layer studied in this research is an industrial paraffin, commonly used in local markets, and its enthalpy–temperature graph is depicted in Figure 4. The fourth model integrated both the SCWF glass and PCMs to explore their synergistic effects. The experimental results were subsequently utilized to validate the accuracy of the simulated models. Figure 5a depicts the recorded air temperature, while Figure 5b shows the variations in solar irradiation intensity.

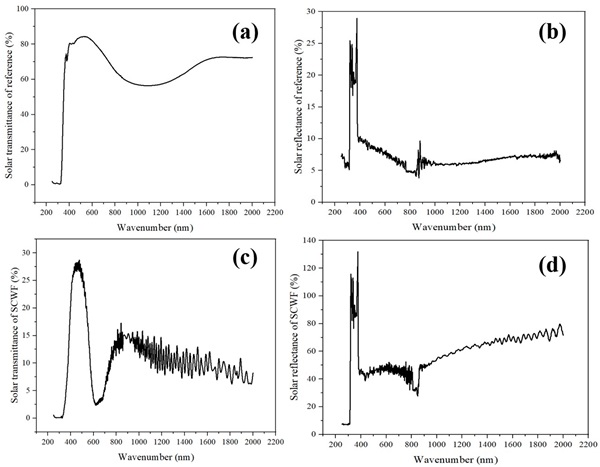
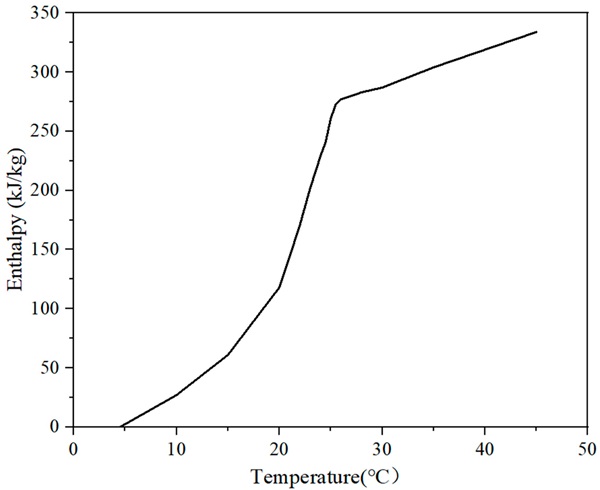
Figure 6 demonstrates a strong correlation between the indoor temperature profiles of the simulated models and those of the experimental models. However, achieving a perfect match between the two curves proves challenging, due to discrepancies in the gathered weather data, which may not precisely align with the data required for the DB software, as well as the limited airtightness of the house models. The deviation ranges of the average indoor air temperature between the simulated and experimental data were calculated using Equation (1). The results revealed that the average deviations (𝑑𝑒𝑣𝑗) of the four room models (i.e., those featuring the reference, only SCWF, only PCM, and both PCM and SCWF model) were 8.77%, 11.29%, 10.81%, and 9.87%, respectively. Accordingly, the established simulation model demonstrates both accuracy and feasibility when utilizing DB software to simulate indoor temperatures.

where 𝑇𝑠𝑖𝑚𝑗 and 𝑇𝑒𝑥𝑝𝑗 represent the simulated and experimental results of the room temperature at hour 𝑗, respectively.

2.2. Simulation Study

2.2.1. Simulation Tool and Mathematical Model

The simulation study was conducted using DB software, which involved discretizing the building envelope into multiple nodes to solve relevant heat transfer equations utilizing an implicit finite difference scheme. This approach allowed for the simulation of heat transport in the presence of PCM [38]. Equations (2)–(5), employed as implicit representations, were utilized to model heat transport within the scope of this study.

The energy consumption of the building was calculated using the Ideal Loads Air System module of DB. The HVAC system for an office building was operated between 9 a.m. and 8 p.m., according to a work schedule. A thermal comfort range of 20 °C to 26 °C was selected.

where 𝐶𝑝 represents the specific heat capacity, in kJ/kg-K. This capacity is updated at each time step using Equation (3); ℎ represents a user-defined function of temperature-dependent specific enthalpy, in kJ/kg; 𝜌 represents the density in, kg/m³; ∆𝑥 represents the finite difference layer thickness, in m; ∆𝑡 represents the calculation time step, in s; 𝑇 represents the node temperature, in K; 𝑖 represents the node being modeled; 𝑖+1 and 𝑖+1 represent the adjacent nodes towards inner and outer sides of the building, respectively; 𝑗+1 and 𝑗 represent the simulation time step and previous time step, respectively; 𝑘𝑊 represents the thermal conductivity for the interface between the 𝑖 node and the 𝑖+1 node, and it is calculated with Equation (4); 𝑘𝐸 represents the thermal conductivity for the interface between the 𝑖 node and the 𝑖−1 node, and it is calculated according to Equation (5).

2.2.2. Building Model Description

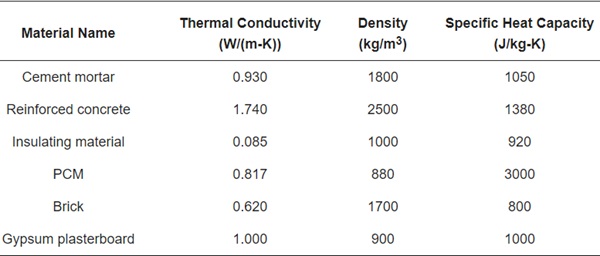
A typical three-story office structure was used for the simulation, as depicted in Figure 7a, in accordance with our previous study [40]. The building comprises three floors, each with a height of 3.30 m and a floor area of 646.58 m² (41.85 m × 15.45 m). The PCM is arranged in the roof, floor, and internal partitions of the building, as indicated with the red lines in Figure 7b. Figure 8 illustrates a schematic of the building components, and Table 1 provides the thermophysical parameters of the building materials.

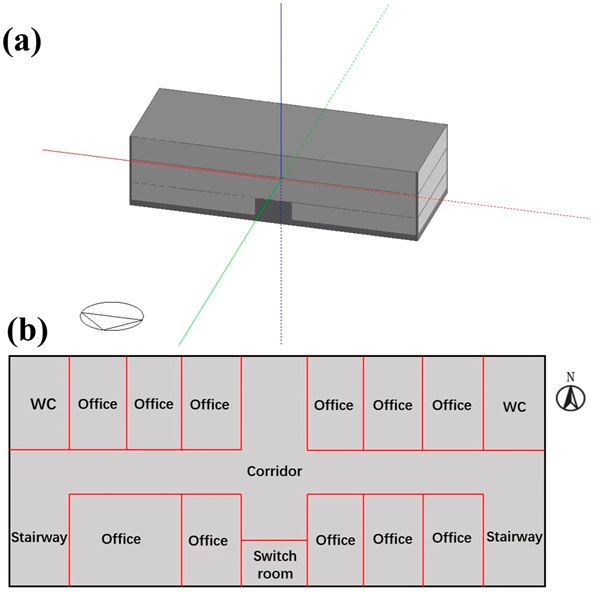
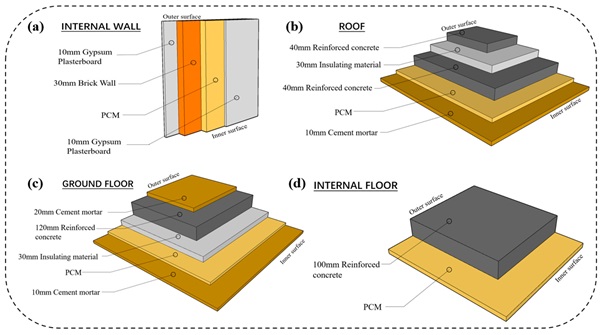
Table 1. Thermophysical properties of the building materials.

2.2.3. Location Selection

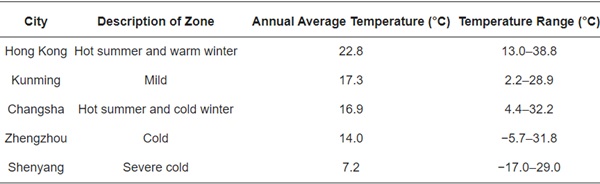
To investigate the effects of different climate conditions on the thermal performance of glass curtain wall buildings with integrated PCM walls, five locations were selected, based on the five types of climates prevalent in China [40]. These sites encompass tropical, subtropical, and temperate zones, showcasing a variety of monsoon and temperature characteristics: (i) Hong Kong, characterized by a tropical monsoon climate with hot and humid summers and cool, dry winters; (ii) Kunming, featuring a subtropical highland monsoon climate with relatively mild temperatures, though experiencing significant temperature differences between day and night (up to 20 °C in winter and 10 °C in summer); (iii) Changsha, with a subtropical monsoon climate marked by warm and rainy seasons; (iv) Zhengzhou, showcasing a monsoon-influenced humid subtropical climate with four distinct seasons; and (v) Shenyang, exhibiting a sub-humid warm continental monsoon climate with four distinct seasons, including a long winter (from November to March) and a short summer (from June to August). Table 2 summarizes the annual average temperatures and temperature ranges throughout the year in the five selected cities. Notably, the temperature differences among the regions are substantial, leading to different demands for cooling and heating. Figure 9 depicts the distribution of these climate zones. The varied climatic conditions serve as a comprehensive foundation for our thorough investigation into the thermal performance of glass curtain wall buildings with integrated PCM.

Table 2. Climate information for the five selected cities.

2.2.4. Parametric Case Studies

In this study, the key parameters crucial for achieving the research objectives of low energy consumption and cost-effectiveness were identified as the SHGC, U-value, and PCM thickness. These parameters play pivotal roles in shaping the thermal performance of buildings. Specifically, the SHGC directly influences the control of solar radiation entering buildings, thereby enhancing energy efficiency and indoor thermal comfort. The U-value significantly impacts the thermal resistance of the building envelope, directly affecting the overall energy consumption. The PCM thickness regulates thermal performance by storing and releasing energy during phase transitions, with economic feasibility being influenced by the high cost of PCMs.

Table 3 provides an overview of the design parameters for glass (SHGC and U-value) and PCM layer thickness characteristics, emphasizing their impacts on energy consumption and thermal comfort, in comparison to the reference case. The specified ranges align with the General Code for Energy Efficiency and Renewable Energy Application in Buildings (GB 55015-2021) [41] and were validated in prior simulations. Some parameters varied within its specified range, while others were maintained at default values.

Table 3. Value range of the three crucial parameters.

To distinguish the distinct influences of phase change and thermal resistance, the heat of fusion value for the PCM was intentionally set to zero. Additionally, the authors of this study explored the variation in energy consumption resulting from different PCM thicknesses. To ensure an unbiased assessment of the impacts of glazing parameters and PCM layers on thermal performance across the five selected climate zones, consistent building envelopes and HVAC systems were applied in all simulated scenarios.

2.3. Sensitivity Analysis and Optimization

To investigate the key factors influencing the annual energy consumption in various cities, a sensitivity analysis was conducted. The authors used this analysis to examine the changes in energy consumption by decreasing and increasing each parameter by 50% relative to its default value, following the methodology outlined by Kishore et al. [23].

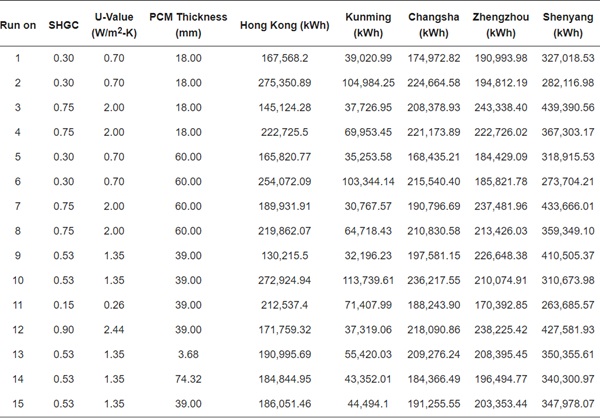
For the enhancement of building design, the aim is to identify the optimal combination of parameters that minimizes energy consumption while considering the cost of the PCM. In this study, Response Surface Methodology (RSM) was employed to scrutinize the relationships between building design parameters (SHGC, U-value, and PCM thickness) and energy consumption. Centered Composite Design (CCD), a subtype of RSM, was chosen for its capacity to concurrently analyze multiple responses and formulate mathematical polynomial prediction models, aiming to determine the optimal solution that meets the desired global optimum. Table 4 delineates the values and coding levels for each variable, while Table 5 outlines the designs of simulation schemes. Subsequently, the relationship between each variable and the energy consumption was determined using the quadratic model presented in Equation (6). Through an analysis of the response surface, the correlation between the quadratic effects and the local form of the response surface can be evaluated, aiding in the identification of the optimal set of design parameters for minimizing energy consumption. Following this procedure, an analysis of variance (ANOVA) statistical analysis for the model was conducted to diagnose its development. Finally, the validated model was employed to identify the optimal factor levels at which the response variable attains its optimal value. To ascertain the optimal combination of parameters aligning with the desired outcomes, the desirability function was employed. The simulation design (y₁, y₂, …, y_m) underwent a transformation into dimensionless values, denoted as individual desirabilities (dᵢ), subsequently amalgamated into an overarching metric, termed overall desirability (D) [42]. A mathematical model was fitted to the D values, providing a comprehensive description of the simulated behavior [43], and the variables under investigation were optimized according to the criterion of minimizing energy consumption. This entire process was executed using the Design Expert software version 13.

Table 4. Factors and their ranges of variation.

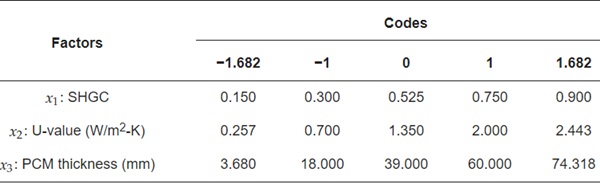
Table 5. The designs of simulation schemes.

However, considering the potential costliness of implementing PCMs, it is crucial to evaluate the cost-effectiveness of this solution. Therefore, alternative parameter combinations were devised, with PCM economics as a primary consideration. This objective comprised the electricity-saving cost of the building (𝐶𝑠), the initial investment cost of the PCM (𝐶𝑝), and the maintenance cost of the PCM (𝐶𝑚). Objective (𝐹) presented the life cycle economic benefit of a PCM-enhanced GCW building, which is expressed as Equations (7)–(10). Equation (11) is used to calculate the difference in life cycle economics between the two objectives of minimum energy consumption and optimal economics. In addition, to assess the accuracy of the predicted annual energy consumption, the absolute relative deviation between the simulated and predicted scenarios was calculated using Equation (12).

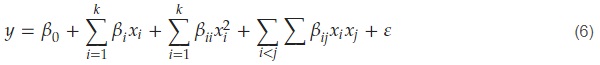
where 𝑦 represents the response variable (in this case, building energy consumption); 𝛽0 is the constant term; 𝛽𝑖, 𝛽𝑖𝑖, and 𝛽𝑖𝑗 are the coefficients of the linear, quadratic, and interaction terms, respectively; 𝑥𝑖 and 𝑥𝑗 are the independent variables (design parameters); ε is the error term.

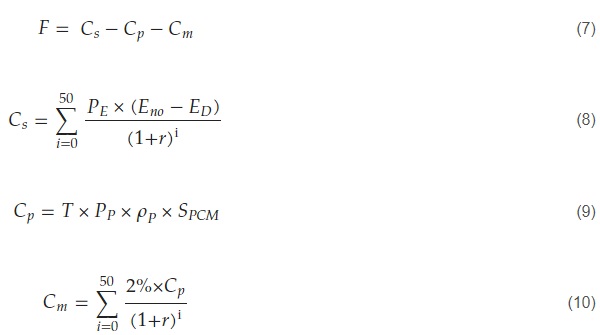
where 𝑃𝐸 is the electricity price is shown in Table 6 [40]; 𝐸𝑛𝑜 is baseline annual energy consumption (SHGC = 0.874, U-value = 1.5 W/m²-K, and without PCM); 𝐸𝐷 is the annual building energy consumption with different optimal designs; r is the discount rate, and 5% is considered in this study [40]; 𝑖 is the service life of a building, usually 50 years [44]; 𝑇 is the thickness of PCM; 𝑃𝑃 is the PCM price, and USD 2/kg is considered in this study [45]; 𝜌𝑃 is the PCM density, and 880 kg/m³ is considered in this study; 𝑆𝑃𝐶𝑀 is the area of PCM arranged in the office building, and 4191 m² is considered in this study.

where 𝐹1 represents the life cycle economic benefit of a PCM-enhanced GCW building under a 50-year service life, targeting the lowest energy consumption; 𝐹2 represents the life cycle economic benefit of a PCM-enhanced GCW building under a 50-year service life, targeting the optimal economic costs; 𝛿 represents the difference in life cycle economic benefits between these two objectives; 𝐸𝐴𝑅𝐷 represents the absolute relative deviation between the annual energy consumption of the simulated schemes and the predicted schemes; 𝐴𝑠 and 𝐴𝑝 represent the annual energy consumption of the simulated schemes and the predicted schemes, respectively.

Table 6. The electricity prices for the five cities.

3. Results and Discussion

3.1. Effect of Building Thermal Efficiency by SHGC

In this section, the analysis focuses on the impacts of the SHGC on the indoor temperature and energy consumption of GCW office buildings in five cities across China. Figure 10 illustrates the substantial influences of SHGC values on energy usage. The SHGC represents the proportion of the solar heat gain coefficient that enters the interior environment, and an increase in the SHGC results in higher heat gain in the building. This indicates the importance of optimizing insulation against solar radiation to enhance comfort levels in hot regions. Conversely, in Shenyang, the lowest energy usage is attained at an SHGC of 0.9, emphasizing the need to maximize solar heat gain in cold climates to reduce the demand for heating. The optimal SHGC value in other regions, such as Kunming, Changsha, and Zhengzhou, falls in the middle range, with a value of 0.3 in Kunming, 0.3 in Changsha, and 0.6 in Zhengzhou. This underscores the importance of balancing solar heat gain in energy consumption in moderate climates. Additionally, due to its dimensionality, Hong Kong exhibits the highest proportion of cooling energy consumption, accounting for 99.87% of its total annual energy consumption. Shenyang has the lowest proportion of refrigeration energy consumption, at 33.01%, followed by Zhengzhou at 69.26%, Changsha at 91.3%, and Kunming at 97.76%.

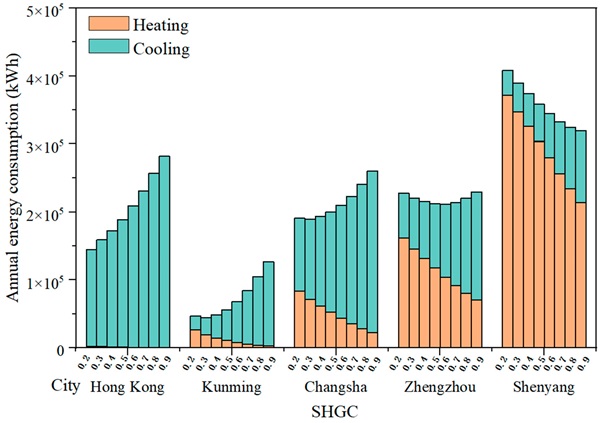
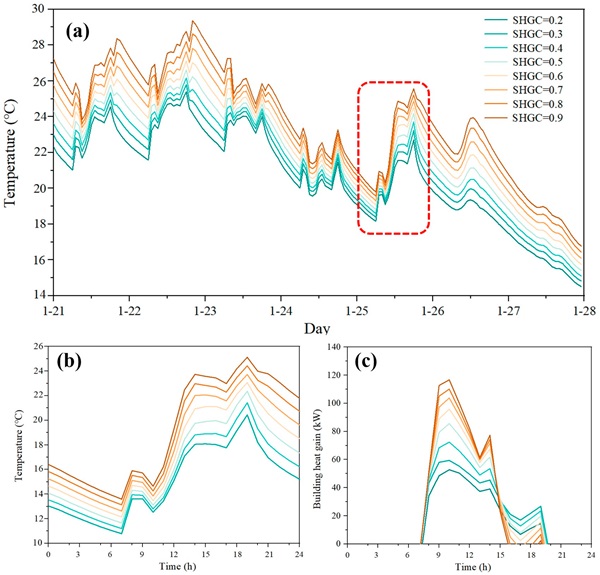
Figure 11 and Figure 12 present the impacts of the SHGC on indoor temperature during a typical week and a day of heat gain in June (summer) and January (winter), respectively, in Hong Kong. The same pattern is observed in all five cities; therefore, the results for the other cities are excluded from the figures for conciseness. As depicted in Figure 11, a lower SHGC has a more pronounced effect on temperature management, resulting in the indoor temperature approaching thermal comfort during the summer. Figure 12 shows that, as the SHGC increases, its influence on temperature regulation becomes more significant, leading to indoor temperatures approaching thermal comfort in winter. Maintaining a low SHGC brings indoor temperatures closer to thermal comfort in summer, while a high SHGC achieves this proximity in winter. In regions where cooling energy is prevalent, choosing glass with an SHGC of 0.2 is recommended for achieving both a comfortable indoor temperature and low energy consumption.

3.2. Effect of Building Thermal Efficiency by U-Value

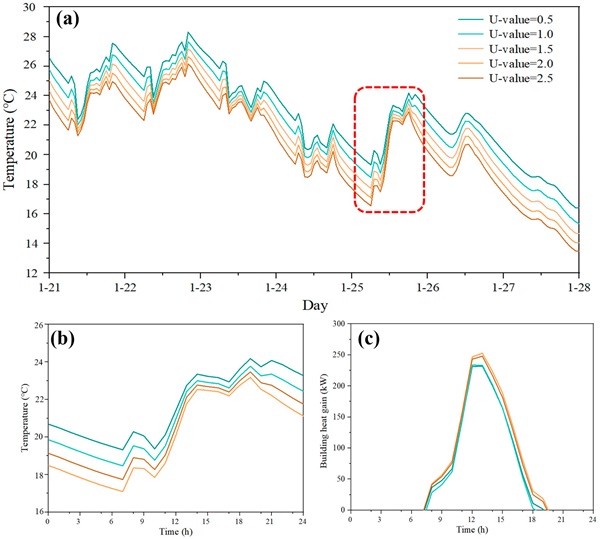
In this section, the indoor temperature and energy consumption of a GCW building in five Chinese cities with varying U-values are examined. Figure 13 compares the annual cooling and heating energy consumption across the cities. The results indicate that, in cold climates (Shenyang and Zhengzhou), energy consumption steadily increases with the rise of the U-value, whereas, in hot climates (Hong Kong, Kunming, and Changsha), the opposite trend is observed. This is attributed to the fact that lower U-values, indicative of better insulation performance, require less heating energy consumption. In cold climatic conditions, the stability of cooling energy consumption is maintained, with the U-value predominantly influencing heating energy consumption. Therefore, a lower U-value is deemed more favorable, as it corresponds to enhanced insulation performance, particularly crucial in mitigating heating energy requirements. However, in warmer climates such as Hong Kong, cooling energy consumption constitutes a larger proportion of the total energy consumption, making a higher U-value more favorable. The optimal U-value for Hong Kong, Kunming, and Changsha is 2.5 W/m²-K, while, for other cities, the optimal U-value is 0.5 W/m²-K. This underscores the importance of thermal insulation in buildings during cold weather and heat resistance in warm weather.

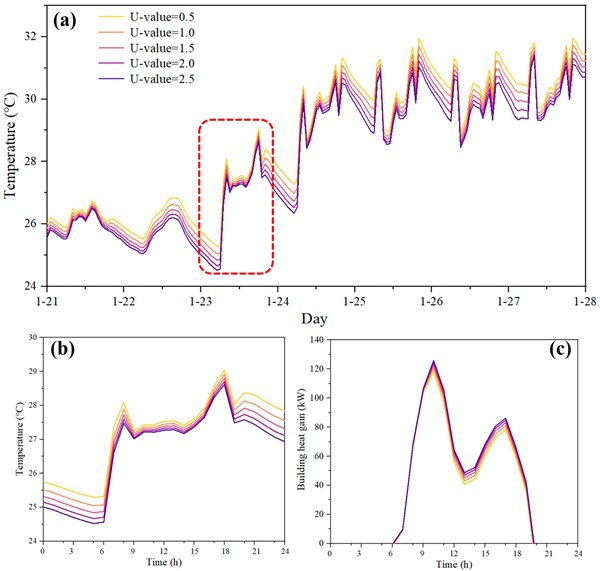
Figure 14 and Figure 15 depict the indoor temperature profile of a glass office building in Hong Kong during a typical week and a day of heat gain in June (summer) and January (winter), respectively. The same pattern is observed in all five cities; therefore, the figures exclude results from the other cities for conciseness. These figures demonstrate that, as the U-value of the glass curtain wall decreases, the indoor temperature approaches the thermal comfort level in summer and increases in winter. The U-value serves as a measure of thermal insulation provided by glazing, for which lower U-values indicate better insulation [43]. As the U-value decreases, less heat enters the building, reducing the heat gain and increasing the indoor temperature. It is noteworthy that the impact of U-values on the highest indoor temperature in summer is only 0.8 °C, while in winter, it is 3 °C. This underscores the dominant role of U-values in winter.

3.3. Effect of Building Thermal Efficiency by PCM Dosage

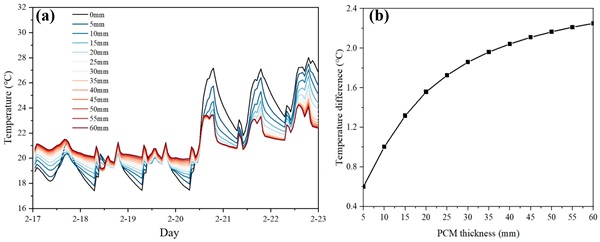
Figure 16 illustrates the impact of PCM thickness on indoor temperature differences in GCW buildings in Hong Kong. With the increasing thickness of the PCM layer, the trend of temperature difference in GCW buildings with or without PCM escalation becomes progressively gradual. The amount of energy stored in the PCM is directly proportional to the volume of PCM used. Consequently, increasing the volume of PCM results in higher energy storage, although there may be a plateau, when the PCM reaches its maximum energy absorption capacity. However, the influences of PCMs on temperature regulation are relatively smooth after the highest point, due to the influence of wall thickness. Previous findings are consistent with previous studies conducted by other researchers [46,47].

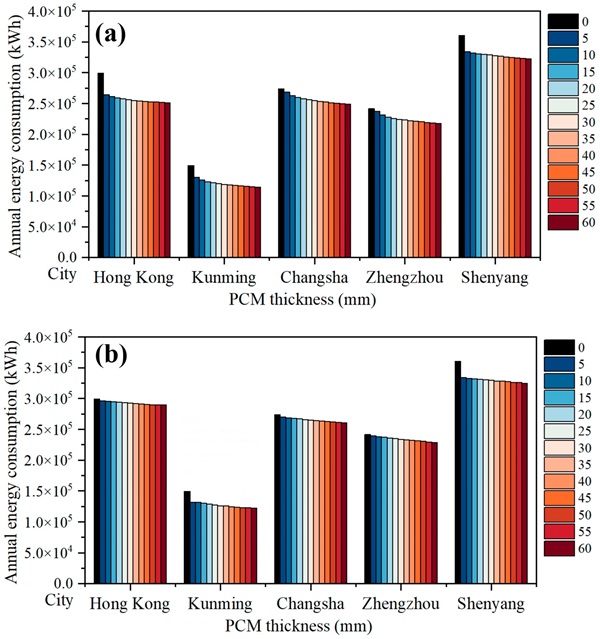
To further investigate the energy-saving potential of PCMs, dynamic simulations were performed for five different locations in China. Figure 17a provides a comparison of energy consumption based on varying PCM thicknesses in these cities. Additionally, Figure 18a demonstrates the relationship between PCM thickness and the energy savings rate (η), as calculated with Equation (13). The findings reveal a substantial increase in the energy savings rate as the PCM thickness is augmented, with a peak efficiency observed at a thickness of 20 mm. Beyond this point, the rate of energy savings exhibits diminishing returns, showing a less pronounced improvement trend. For instance, in Kunming, the annual building energy consumption decreased by 13.09%, 15.98%, 17.69%, 18.97%, and 19.88% when PCM thicknesses of 5 mm, 10 mm, 15 mm, 20 mm, and 25 mm were implemented, respectively. Therefore, a PCM layer thickness of 20 mm was deemed the most effective, providing an energy savings rate of approximately 19% while requiring a smaller volume of PCM. The solar heat gained by the building corresponds to a specific quantity of PCM, indicating that the PCM’s effect reaches its maximum utilization at a certain thickness. Further enhancements in PCM efficiency can be attributed to the impact of thermal resistance. At this juncture, it is not recommended to further increase PCM thickness.

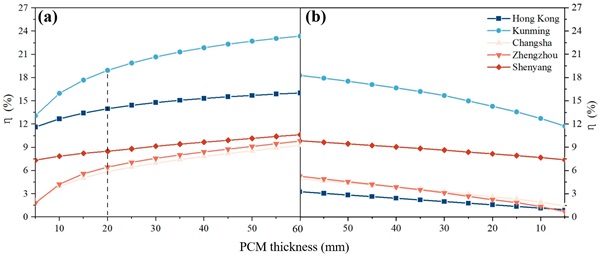
Furthermore, to elucidate the distinct influences of phase change and thermal resistance changes on energy performance, the enthalpy of the PCM was deliberately set to 0, with the results depicted in Figure 17b and Figure 18b. The outcomes suggest that the influence of thermal resistance appears to follow a linear trend, contrasting with the non-linear effects of phase transition. Furthermore, with an increase in PCM thickness, both PCM effects and thermal resistance become significant. However, the proportions of their influences vary across different climatic zones. For instance, in Hong Kong, the enthalpy-based energy savings rate ranges from 0.93% to 3.25%, while the entropy-based savings rate reaches a significantly higher range, from 11.63% to 16%. This observation underscores that the impacts of PCM effects constitute a substantial portion of the overall effect.

where no PCM is the baseline of the annual building energy consumption of an SHGC = 0.874, a U-value = 1.5 W/m²-K, and no PCM.

3.4. Sensitivity Analysis

For this section, a sensitivity analysis of annual energy consumption was performed for different climate zones and building characteristics. Figure 19a,b show the energy consumption for each parameter when decreasing/increasing it by 50% from the default value. The results indicate that different factors have varying degrees of influence on the energy consumption in different regions. For hot regions (Hong Kong, Kunming, and Changsha), the SHGC emerges as the most influential parameter. Reducing solar radiation and heat gain in these regions leads to a reduction in cooling energy demand, but an increase in heating energy consumption. Conversely, in Zhengzhou and Shenyang, the U-value has the greatest impact on the annual energy consumption, especially in cold climate zones, where the U-value exhibits a more pronounced effect compared to the SHGC. Regardless of whether the U-value is decreased or increased by 50% from the default value, the average annual change in energy consumption is notable: 10.5% in Hong Kong, 20.2% in Kunming, 31.6% in Changsha, 9.3% in Zhengzhou, and 14.4% in Shenyang. These results underscore the considerable influence of the U-value on the annual energy consumption, particularly in cold climate zones.

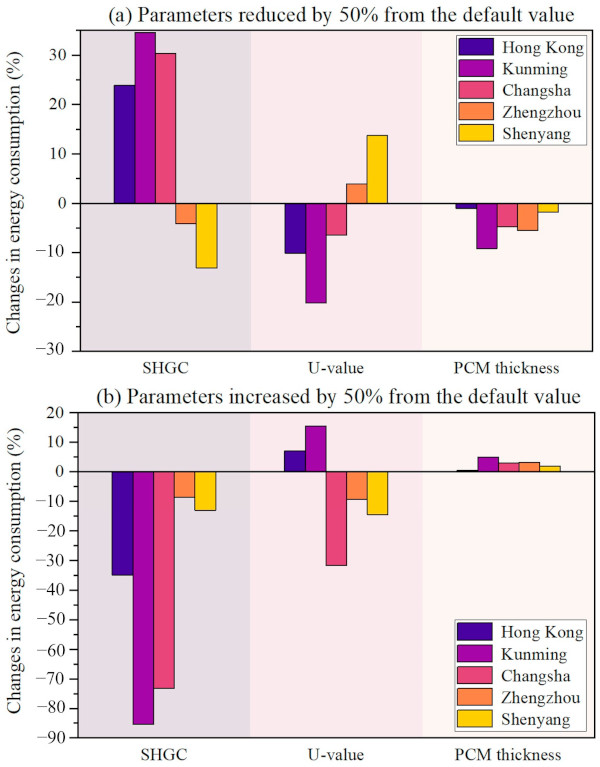
Additionally, it was observed that annual energy consumption exhibited an inverse proportionality to the thickness of the PCM, indicating that thicker PCM resulted in lower annual energy consumption. This relationship was most pronounced in Kunming, where the temperature difference between day and night is significant during both winter and summer. However, the impacts of PCM parameters on energy consumption are minimal (less than 5%) in other cities. This can be attributed to the fact that the temperature in Hong Kong often exceeds the PCM phase transition temperature, while the temperature in Shenyang is below the phase transition temperature. Because Changsha and Zhengzhou have warm climates with small diurnal temperature differences, the effects of PCMs are limited.

3.5. Response Surface Method Optimization

3.5.1. Optimization Model Analysis

As shown in Table 7, regression equations of the first-order quadratic polynomial model were established to determine the relationships between variables and the annual energy consumption in each of the five cities. The ANOVA presented in Table 8 indicates that all models have a good fit, with p-values below 0.05. Furthermore, the high coefficient of determination (R²) values, of 0.9354 or higher, confirm the accuracy of the developed models, exceeding the recommended threshold of 0.80 [48]. The predicted correlation coefficient (Predicted R²) and adjusted correlation coefficient (Adjusted R²) fall within acceptable ranges, indicating the validity of the established models when the difference between the Predicted R² and Adjusted R² values is less than 20%. The Adequate Precision value, measuring the Signal-to-Noise Ratio, is ideal at 22.12 or higher. Figure 20 presents alignment along a nearly identical line. These results validate the accuracy of the quadratic model in predicting the annual energy consumption of GCW buildings within the range of simulated factors.

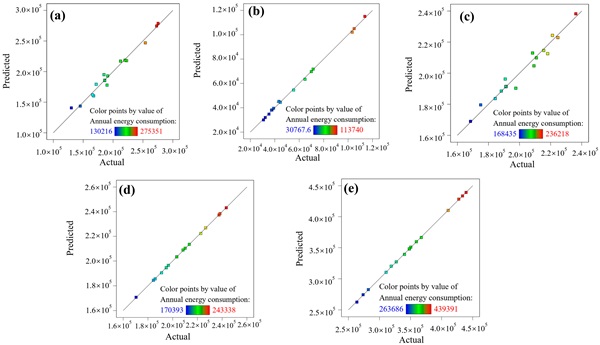
Table 7. The relationships between variables and the annual energy consumption.

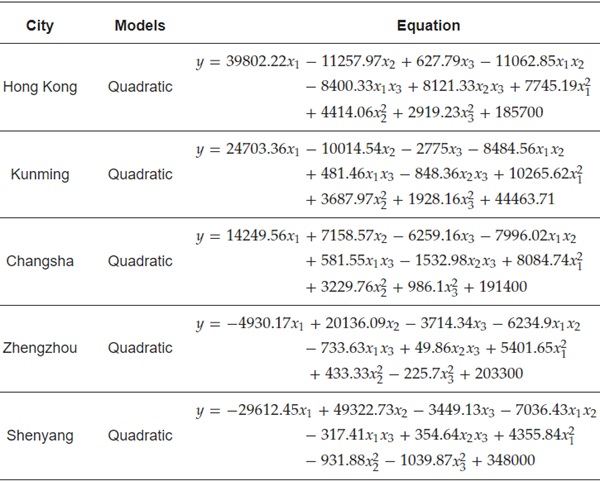
Table 8. The analysis of variance statistics of the models.

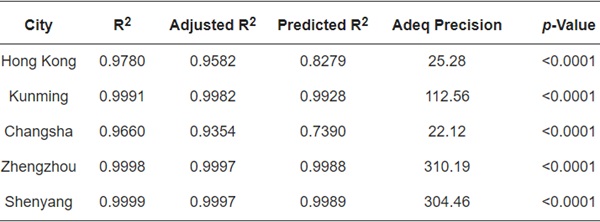
Figure 21, Figure 22 and Figure 23 further illustrate the relationships between each variable and the annual building energy consumption for five cities. In Figure 21, the influences of the SHGC and the U-value on the annual energy consumption are depicted, with exceptions for Zhengzhou and Shenyang, where energy consumption increases with a rising SHGC when the U-value is 0.5 W/m²-K. Figure 22 highlights the interactions of the SHGC and PCM thickness on the annual energy consumption. Notably, when the thickness of PCM is 5 mm, the energy consumption in Kunming and Changsha initially decreases, and then increases with the rise of the SHGC. Figure 23 demonstrates the interactions of the U-value and PCM thickness on the annual energy consumption. Analyzing the mutual influence of each variable aids in the interpretation of results obtained through the subsequent expectation function method.

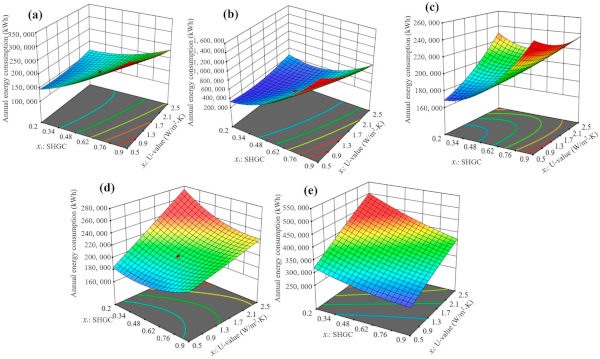
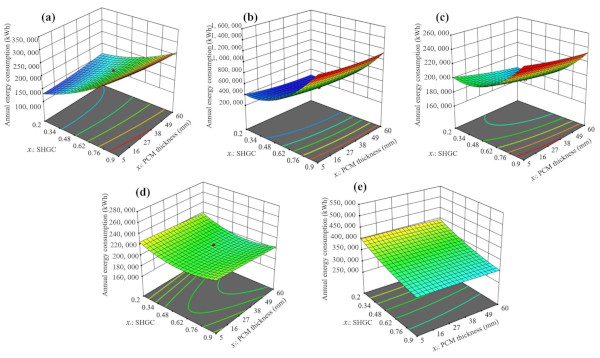
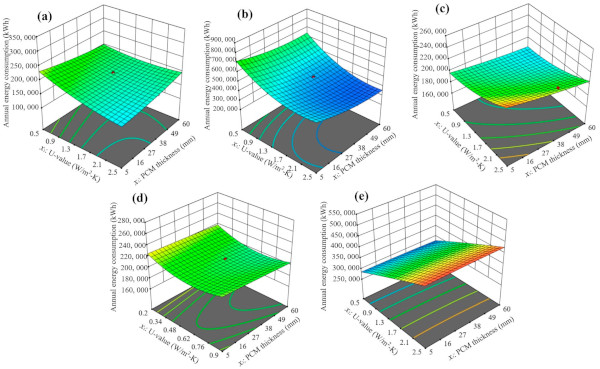
3.5.2. Optimal Scheme Analysis

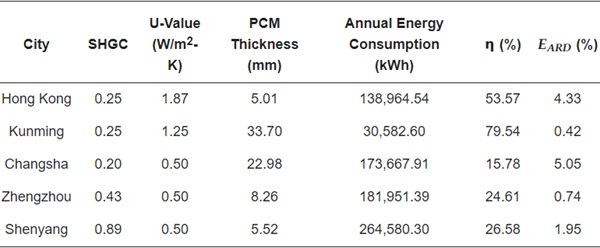
To minimize the annual energy consumption, the expected function method was utilized in RSM, setting the target response as the minimum building energy consumption. The findings in Table 9 demonstrate that the optimal parameter configuration varies, based on the specific characteristics of each city. Nevertheless, across all cities, consistently achieving minimum energy consumption is associated with a PCM thicknesses close to 60 mm. This optimal combination of parameters demonstrated its effectiveness in reducing energy consumption during both summer and winter by utilizing the energy storage capacity of PCMs and modifying the glazing characteristic parameters. In addition, the energy-saving rate of the optimal parameter combination was calculated using Equation (13). The results demonstrated energy savings ranging from 20.16% to 81.18% in different regions of China.

Table 9. Optimal parameter configurations.

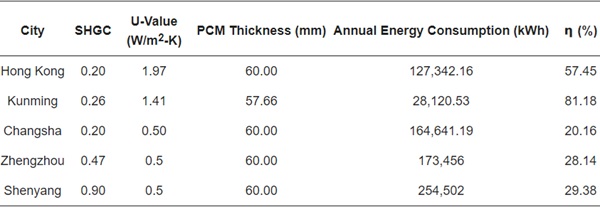
Table 10 presents the life cycle economics of PCM-enhanced GCW buildings, considering two objectives: the lowest energy consumption and the optimal economic cost. Additionally, it can be observed that the difference in life cycle economic benefits ranges from 5.49% to 25.65%. Table 11 presents the optimal combination of parameters after considering the economic costs and their corresponding annual energy consumption. These optimized parameters result in energy savings ranging from 15.78% to 79.54% in different regions of China. While these fall below the scenario with the minimum energy consumption target, the achieved savings remain considerable. Furthermore, the results of absolute relative deviation between the simulated and predicted schemes indicate a deviation (𝐸𝐴𝑅𝐷𝐸𝐴𝑅𝐷) of less than 6%, confirming the reliability of the predicted values.

Table 10. The life cycle economics of PCM-enhanced GCW buildings.

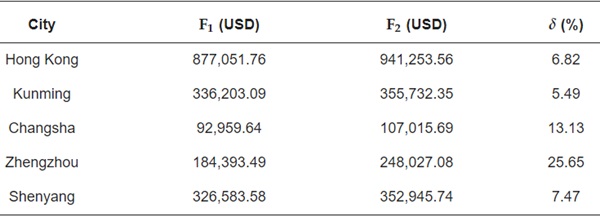
Table 11. The optimal combination of parameters after considering economic costs.

4. Conclusions and Limitations

4.1. Conclusions

In this study, the building thermal performance and the energy consumption resulting from applying PCMs in GCW buildings with various glazing parameters, including the SHGC and the U-value, were evaluated. Additionally, optimization parameter designs were performed to enhance the energy efficiency and economic benefits of PCM-enhanced glass curtain wall buildings. The key findings can be summarized as follows:

1. The investigation of PCM thickness in GCW buildings revealed that, with increasing PCM layers, indoor temperature differences are reduced and energy storage is enhanced. Optimal energy savings were achieved with a PCM thickness of 20 mm, which resulted in a 19% reduction in the annual energy consumption, while further increasing thickness showed diminishing returns in energy efficiency.
2. The sensitivity analysis revealed that the SHGC is the most influential parameter in Hong Kong, Kunming, and Changsha. The U-value has the greatest impact on the annual energy consumption in Zhengzhou and Shenyang. These findings highlight the critical factors affecting the energy consumption in different regions.
3. The relationships between the SHGC, the U-value, and PCM thickness and energy consumption was established using RSM. The optimal parameter combinations were applied to GCW buildings in China, and significant energy savings, ranging from 15.78% to 79.54%, were achieved. Among them, the life cycle economic benefits ranged from 5.49% to 25.65%. These findings provide valuable guidance for building projects in different climate zones in China.

4.2. Limitations

Despite the significant insights gained from this study, several limitations should be acknowledged:

1. This study did not account for the cost of glazing, or the carbon emissions associated with glazing production. This omission was attributed to the substantial variability in production costs and processes among different glazing manufacturers. Future research should encompass these aspects to enhance the economic payback period and overall utilization efficiency of PCMs.
2. This study focuses mainly on proposing novel design concepts and methods to optimize the parameters of GCW buildings. Although it provides a strong framework for improving energy efficiency, other factors, such as occupant comfort, architectural aesthetics, and the building characteristics of different regions should be considered in practical applications.
3. This study relies on certain assumptions inherent to the RSM model, including the linearity of relationships between variables and the uniformity of the design space. Specifically, the method assumes a smooth and continuous response surface, and the effectiveness of the model may be influenced by the specific characteristics of the studied system. Therefore, caution should be exercised when extending these findings to various building types or non-linear systems.

Author Contributions

Conceptualization, H.Y. and H.C.; data curation, H.Y. and Y.Z.; formal analysis, X.Z., Y.L. and Y.Z.; methodology, X.Z., Y.L. and H.C.; supervision, H.C.; writing—original draft, X.Z.; writing—review and editing, H.Y. and H.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was fully funded by a grant from the Natural Science Foundation of China (Grant No. 51925804), the Shenzhen Science and Technology Program (Grant No. KQTD20200909113951005), and the National College Student Innovation and Entrepreneurship Training Program (Grant No. 202210590041).

Data Availability Statement

All data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References