Structural Topology Optimization for Abrasive Water-Jet Fabricated Glass

Article Information

• Digital Object Identifier (DOI): 10.47982/cgc.9. 485
• Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess.
• Published as part of the peer-reviewed Challenging Glass Conference Proceedings, Volume 9, June 2024, 10.47982/cgc.9
• Editors: Christian Louter, Freek Bos & Jan Belis
• This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
• Copyright © 2024 with the author(s)9

Authors:

• Kimhong Heng - Univ. Rennes, CNRS, IPR (Institut de Physique de Rennes) - UMR 6251
• Maxime Vassaux - Univ. Rennes, CNRS, IPR (Institut de Physique de Rennes)
• Raveth Hin - Research and Innovation Center, Institute of Technology of Cambodia, Phnom Penh
• Chansopheak Seang - Research and Innovation Center, Institute of Technology of Cambodia, Phnom Penh
• Eric Robin - Univ. Rennes, CNRS, IPR (Institut de Physique de Rennes)
• Jean-Christophe Sangleboeuf - Univ. Rennes, CNRS, IPR (Institut de Physique de Rennes)

1.Introduction

Glass has been used in modern architecture and civil engineering for various applications. The significantly high self-weight of today’s glass products is a critical factor for connections and wide-span design (Hänig and Weller 2020). Heavyweight also introduces significant challenges during the transportation and installation stages, requiring careful planning, resources, and expertise to overcome. Moreover, addressing the high usage of materials in the construction industry is a major concern of CO2 emissions (Choi et al. 2017). This seems to be unsustainable for using glass in the construction industry. Hence, lightweight glass structures with curved shapes or hold filling in the structures are a key leading to highly innovative glazing solutions (Belis et al. 2019; Louter et al. 2018; Silveira et al. 2018). 

Currently, the development of lightweight design strategies for glass structures is based on the composite laminate concept (Hänig and Weller 2020, 2021, 2022; Kothe et al. 2021; Pfarr and Louter 2023; Shitanoki et al. 2015) which is applied to most structural glass applications. Combining a strong glass material with a robust interlayer material can result in thin structural composite glass panels.

Alternatively, topology optimization is an innovative structural design solution that may enable to design of lightweight structures and structural shapes for a wide range of application purposes. The challenge of topology optimization design for glass can be both fabrication and computational design as the optimized structure has irregular shapes and the solution of topology optimization obtained from mathematical programming and finite element techniques is computationally intensive (Giraldo-Londoño et al. 2022). 

From the latest advancements in glass fabrication methods, 3D printing of glass can create small-scale glass objects, as demonstrated by Inamura et al. (2018) and Klein et al. (2015). For larger-scale structures, 2D structural glass shapes are rather fabricated using abrasive water-jet (AWJ) or laser cutting techniques, as noted by Nisar et al. (2013). These cutting methods enable the fabrication of structures as large as the size of the largest available glass product. Furthermore, the cut glass pieces can be laminated to enhance safety and structural integrity. By combining advanced cutting methods with lamination techniques, it may become possible to create large-scale 3D structural glass assemblies. This approach is akin to brick construction, where individual components are assembled to form a cohesive structure. In our topology optimization approach, we will rely on mechanical properties characterised specifically on AWJ cut glass.

Recently, a few research efforts have been made to enable structural topology optimization for such a brittle material. In turn, enabling the design of cast glass structures such as bridges, slabs, shells, and connections (Damen et al. 2022; Daniella 2020; Koopman 2021; Stefanaki 2020). The studies mainly focused on the application of commercial topology optimization tools to design mass-optimized structures to reduce the annealing time for the fabrication process. The design was based on compliance-based (elastic energy) or Von Mises stress-based optimization. In such cases, compliance optimization is related to stiffness optimization. Von Mises stress is often appropriate for evaluating the failure of ductile materials (Duysinx and Bendsoe 1998). 

Now for brittle materials specifically, there are very few topology optimization developments based on maximum principal stress. The majority of research works have adopted the Von Mises stress. Nonetheless, Chen et al. (2021) developed global maximum principal stress-constrained topology optimization based on the Bidirectional Evolutionary Structural Optimization (BESO) method for 2D concrete structures. The p-norm aggregation function was used to compute the peak stress value and was constrained to be smaller than the stress limit. Using an aggregation function in stress-constrained topology optimization is an effective technique for collecting millions of constraints to one constraint(Bendsøe and Sigmund 2003; Duysinx and Sigmund 1998; París et al. 2009). However, the aggregation function estimates the value greater than the real maximum value. 

Moreover, solving the volume minimization problem under stress constraints by the BESO method may not be achieved because the optimizer algorithm requires a predefined volume (Querin et al. 2017). Later, Giraldo-Londoño et al. (2022) proposed another topology optimization algorithm based on local maximum principal stress constraints solved by Solid Isotropic Material with Penalization (SIMP) method for 2D and 3D structures. In these recent studies, the maximum principal stress constraint alone could not enable the optimization to converge, thus the classical compliance objective was added to reach local minima. Compliance optimization allows to control indirectly structural displacement which is a limiting factor in structural engineering design. Otherwise, controlling displacement from compliance optimization design is not an effective solution because many compliance optimization design cases have to be tested to reach a predefined displacement condition. Lastly, we observe that self-weight load was neglected in the previous studies while it is an important design load in structural civil engineering design (Zhang et al. 2021) which influences optimal topologies obtained from the SIMP method(Bruyneel and Duysinx 2005).

Thus, the purpose of this work is to implement an algorithm to perform topology optimization for glass structures fabricated by the AWJ cutting method. We focus on the volume minimization problem which is equivalent to weight minimization by considering maximum principal stress and displacement as the design criteria. Self-weight load is also included in our optimization process. Moreover, a scaling coefficient introduced by Le et al. (2010) is used to treat the p-norm aggregation function. This formulated topology optimization algorithm is suited for real engineering design situations and differs from topology optimization performed in previous works (Chen et al. 2021; Giraldo-Londoño et al. 2022). The SIMP method is used to solve our topology optimization problem. To validate numerical results, the mechanical performance of the optimized design structure is verified with the commercial FE software ABAQUS. 

The remaining parts of this paper are organized as follows: computational method including SIMP topology optimization method, stress and displacement aggregation, and topology optimization problem is presented in section 2. The mechanical characterization of glass used in our numerical study is described in section 3. Two numerical examples are demonstrated to show the effectiveness of our algorithm in section 4. Lastly, a conclusion is drawn in section 5. 

2. Computational method

This section presents a topology optimization method framework with a finite element method. Then, an aggregation technique is introduced to estimate the peak value instead of using the max(.) operator in the optimization problem. Then topology optimization problem is introduced. The latter is a computational optimization algorithm.

2.1. Topology optimization

Regarding topology optimization design, we address two structural behaviours and one physical property such as a peak of maximum principal stress, a maximum vertical downward displacement, and a total volume equivalent to the weight or mass of a structure, respectively. Stress and displacement are chosen because this commonly happens in structural engineering design criteria.

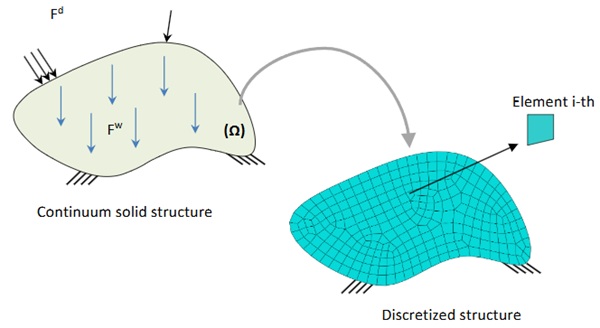
Volume allows to reduce the weight of the structure under a set of predefined conditions. To compute such properties, the structure that is under a set of applied and self-weight loads and boundary conditions in a design region (Ω) as seen in Fig. 1, is discretized into finite elements. With this discretised technique, each finite element has the same brittle linear isotropic material properties and elemental area (2D) or volume (3D). In this work, each finite element has the same square and cube shape for 2D and 3D structures, respectively.

The mechanical behaviour of the solid structure can be evaluated from the nodal displacement of each element which is computed following the equilibrium FE equation below:

where 𝐾 is the global stiffness matrix, U is the global nodal displacement vector, 𝐹𝑤 is the global self-weight force vector, and 𝐹𝑑 is the global applied force vector.

We used a density method to find the optimized structure. In this method, each finite element has a design density variable, 𝑥𝑖∈[0,1], which represents the structure by 𝑥𝑖= 0 is void, 𝑥𝑖= 1 is a solid glass material, and 0 <𝑥𝑖< 1 is intermediate material. To minimize intermediate material which is known as the grey material and to solve checkerboard and mesh-dependency problems in the density method (Sigmund 1994), the robust filtering method (Guest et al. 2004; Sigmund 2007; Wang et al. 2011) is applied to the design variable, 𝑥𝑖. The modified density is now called physical density variables, 𝑥̿𝑖, defined by: 

Here, 𝜂 is a threshold value, 𝛽 is the projection parameter, 𝑁𝑒,𝑖 is the neighborhood set of elements within the allowable filtering region of radius, 𝑟𝑚𝑖n, 𝑟𝑗 is the central distance from element i-th to element j-th, x𝑖 is the filtered density variable obtained by:

and 𝑤𝑗 is the weighting function defined as: 

The total volume ratio, stiffness, and self-weight load of the structure are now formulated to be the functions of physical density variable and can be computed by following:

where 𝑉𝑡otal is the total volume ratio of the structure, 𝑉₀ is the total volume of the initial design structure, 𝑛el is the total number of finite elements, ⋃(∙) is the assembly operator matrix for the global stiffness matrix, v𝑖 the elemental area (2D) or volume (3D), 𝐸𝑖(𝑥̿𝑖) is the interpolation function for stiffness of element i-th, 𝑘𝑖 is the stiffness matrix of element i-th that can be obtained by Gaussian integration, 𝐵𝑖 is a strain-displacement matrix of element i-th that can be obtained from the shape function based on displacement-based finite element, 𝐷₀ is the constant elastic constitutive matrix of the solid material, ∏(∙) is the assembly operator vector for the global self-weight force vector, 𝐹ᵢ𝑤 is the nodal self-weight force vector of element i-th, 𝜌₀ is the physical density of the material, and 𝑔 is the gravitational acceleration (9.81 m/s²).

In this work, the interpolation function for stiffness, 𝐸𝑖(𝑥̿𝑖) is based on the modified SIMP (Bruyneel and Duysinx 2005; Sigmund 2007) defined as below: 

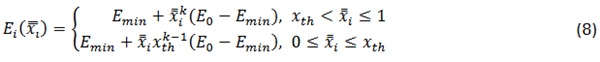
where 𝑥𝑡ℎ is the threshold density value, 𝑘 is the penalty factor for the SIMP model, 𝐸𝑚𝑖n is Young’s modulus of void elements, and 𝐸₀ is Young’s modulus of solid elements. 

2.2. Stress and displacement aggregation

The largest value of maximum principal stress and vertical downward displacement are computed by using an approximated function, the p-norm function below:

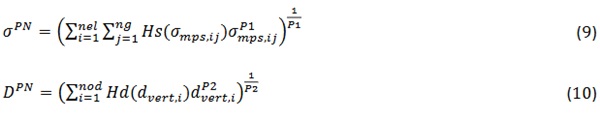
where 𝑛𝑔 is the number of stress evaluation points of an element i-th, in this study 𝑛𝑔=5 points for 2D element and 𝑛𝑔=9 points for 3D element, 𝑛o𝑑 is the total number of finite element nodes, 𝜎𝑚ps s the maximum principal stress, 𝑃1 is the p-norm power of stress, 𝑑𝑣𝑒r𝑡 is the nodal vertical displacement, 𝑃2 is the p-norm power of displacement, 𝐻s(∙) is the Heaviside step function used to eliminate compressive stress defined by: 

and 𝐻𝑑(∙) is the Heaviside step function used to eliminate upward vertical displacement defined by: 

As the p- norm function provides the estimated maximum value greater than the real maximum value obtained from the max(.) operator, a scaling coefficient, 𝑐 introduced by Le et al. (2010) is used to approximate the maximum value by: 

The scaling coefficient, 𝑐𝑐 is computed iteratively by:

Here, 𝑛 is the number of iterations, 𝛼 is a parameter controlling the scaling coefficient, 𝑐 between iterations, in this study 𝛼=0.5 for all iterations, and 𝑐⁰𝑚ps=𝑐⁰𝑑=1. 

Similar to stiffness, the maximum principal stress is multiplied by a relaxation coefficient to avoid stress singularity (Le et al. 2010) and is defined below:

where 𝑄 is the stress relaxation factor and 𝜎⁰𝑚ps,𝑖𝑗 is the maximum principal stress of element i-th evaluated at point j-th. 

2.3. Topology optimization problems

With the above topology optimization method framework, we define a mathematical expression for a volume minimization problem under stress and displacement constraints given by: 

where 𝐷l𝑖𝑚 is the allowable vertical downward displacement and 𝜎l𝑖𝑚 is the predicted failure stress of glass.

2.4. Computational algorithm

The finite element and filtered density developed by Andreassen et al. (2011) and Liu and Tovar (2014)are used in our algorithm development code for 2D and 3D structures, respectively. The Method of Moving Asymptote (MMA) proposed by Svanberg (1987) is used as the standard optimizer. The optimization algorithm is summarized as follows:

1. Initialization state: design domain, loading, boundary conditions, material properties, SIMP, filtering, iteration parameters
2. Discretize the design domain into FE and solve the finite equation to obtain displacement, U
3. Compute the objective function, constraints, and sensitivities
4. Start iteration to meet optimization conditions
5. Update design variable by MMA optimizer
6. Check iteration convergence, the change in design variables 
7. Go to step 3 if iteration convergence does not reach

3. Mechanical characterization of glass material

A float glass sheet with a thickness of 5 mm was mechanically cut by an AWJ machine (Flow Mach2-2030c) into rectangular beams with dimensions of 100 × 10 mm² to evaluate the failure stress through a 3-point bending test as shown in Fig. 2. In this experiment, a universal testing machine Lloyd LR 50K connected with a loading cell of 1 kN was used. The test was performed on 12 beams without polishing at the room temperature of 22 °C. The processed edge of the glass beams was placed on the two similar steel support half rollers with a radius of 5 mm and a bending span of 64 mm. The thickness of glass is the width of the beams. The mid-span loading was applied through a spherical tip cone indenter along the beam width. The loading rate was set as the displacement imposing with a rate of 0.50 mm. The failure force was automatically detected by the machine. The failure strength of each specimen was calculated at the mid-span and defined by the flexural tensile stress below:

where 𝐹𝑓 is the failure force, l is the bending span, ℎ is the height of the beam, and 𝑡 is the width of the beam.

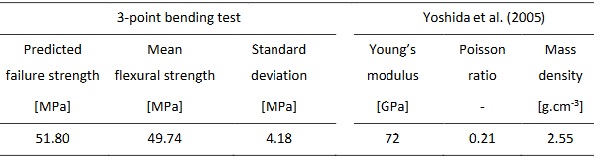
As glass is a brittle material, the stress distribution of specimens does not fit with the normal distribution. The predicted failure stress of glass was calculated by using Weibull statistics at the failure probability of 63%. The reader is directed to (Bergman 1984; Sullivan and Lauzon 1986) for further information on how to characterize brittle material strength with Weibull distribution. Table 1 shows the experimental results of the 3-point bending test and other properties such as Young’s modulus, Poisson ratio, and mass density that were obtained from the previous research.

Table 1: Mechanical properties of float glass used in optimization.

4. Numerical results

This section outlines the results of our implementation of the method introduced in section 2. The calculation is carried out in MATLAB R2023a. Two numerical examples are presented. All the calculation is run on a cluster with an Intel(R) Xeon Gold 6348R CPU @ 2.6GHz and 503GB of RAM. The following parameters are used in all case examples. Material properties are taken from Table 1. Young’s modulus of the void element is 10⁻³ MPa. Filtering parameters, 𝜂=0.5 and 𝛽 is double increased from 1 until 𝛽𝑚a𝑥=16 for every 50 iterations. The p-norm power used for displacement and stress constraints is 40. Stress and SIMP penalty power are 0.5 and 3, respectively. Lastly, threshold density, 𝑥𝑡ℎ is 0.20. The optimized results combined with a numerical validation of a 2D optimized structure demonstrate the efficacy of our topology optimization.

4.1. 2D MBB beam 

The first example is the MBB (Messerschmitt–Bölkow–Blohm) beam subjected to self-weight load and a point load F = 918 N at the mid-span as illustrated in Fig. 3. The height and length of the beam are 100 mm and 500 mm, respectively. Only a half part is optimized as the beam structure is symmetric. The half-MBB beam is discretized into 100 × 250 elements with a surface area of 1 × 1 mm² for each element. The load F/2 is distributed equally on three nodes to avoid stress singularity at the loading point. The symmetric support is constrained on the nodes along the height of the beam. The end roller support is constrained on two nodes. The displacement limit is set to 0.80 mm and the filtering radius is 𝑟𝑚𝑖n=6 mm.

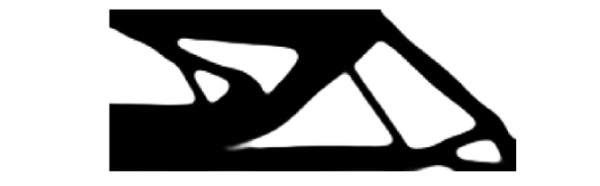
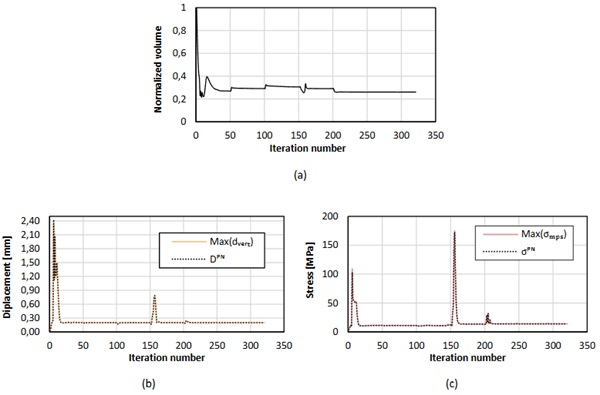
Fig. 4 shows the volume-optimized half-MBB beam. The minimized volume is 0.62% of the original half-MBB beam. The evolutions of volume, stress, and displacement with iteration are presented in Fig. 5 (a-c), respectively. The optimized results show that both stress and displacement constraints satisfythe limit conditions and are close to the limit bounds. The p-norm stress and displacement at the optimum state are 51.75 MPa and 0.7997 mm, respectively. These values are close to the real maximum values obtained from the max(.) operator which are 51.94 MPa, and 0.7996 mm, respectively. This shows the aggregation technique combined with a scaling coefficient approximatesefficiently the peak value. The real maximum stress value is greater than the stress limit of 0.27%. Compared to stress in the original half-MBB structure, topology optimization can minimize the maximum stress from 65.42 MPa to 51.94 MPa as shown in Fig. 6 (a). This reveals that topology optimization for glass can improve structural performance with a significant weight reduction.

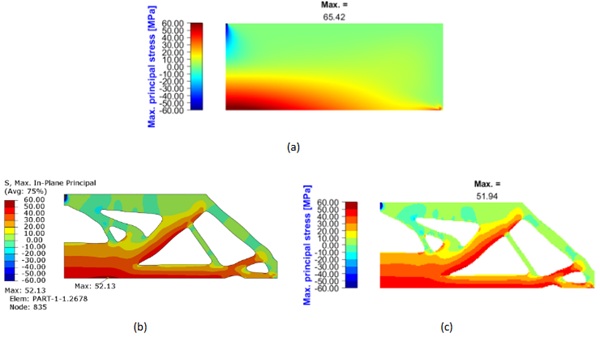
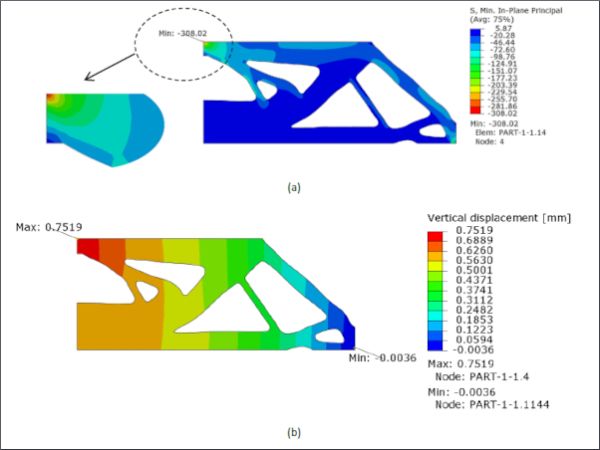
The contour of the optimized half-MBB beam is extracted with a density threshold value of 0.3 to verify mechanical behaviour with FE ABAQUS 2023. The contour coordinates are fitted by the Spline in ABAQUS sketching. 4-node quadrilateral finite elements with arbitrary shapes are used to discretize the beam. Fig. 7 illustrates the geometry, discretized shape, and loading and boundary models of the beam employed for the validation. In this numerical validation, material properties, loading, and boundary conditions are the same as in the optimization design. As seen in Fig. 6 (b), the maximum stress obtained from FEA ABAQUS is 52.13 MPa greater than the stress limit of 0.63%. Both maximum principal stress distribution maps obtained from FEA ABAQUS and the customized optimization tool are quite similar as shown in Fig. 6 (b) and (c), respectively. Moreover, the smallest value of minimum principal stress and maximum vertical downward displacement of FEA ABAQUS are -308.02 MPa and0.7519 mm as depicted in Fig. 8 (a-b), respectively. This shows that the post-processing does not influence the optimized results. The minimum value of minimum principal stress is still below the range of the compressive stress limit of 1000 MPa of float glass (Ashby and Jones 2013) even though there is no constraint on this stress.

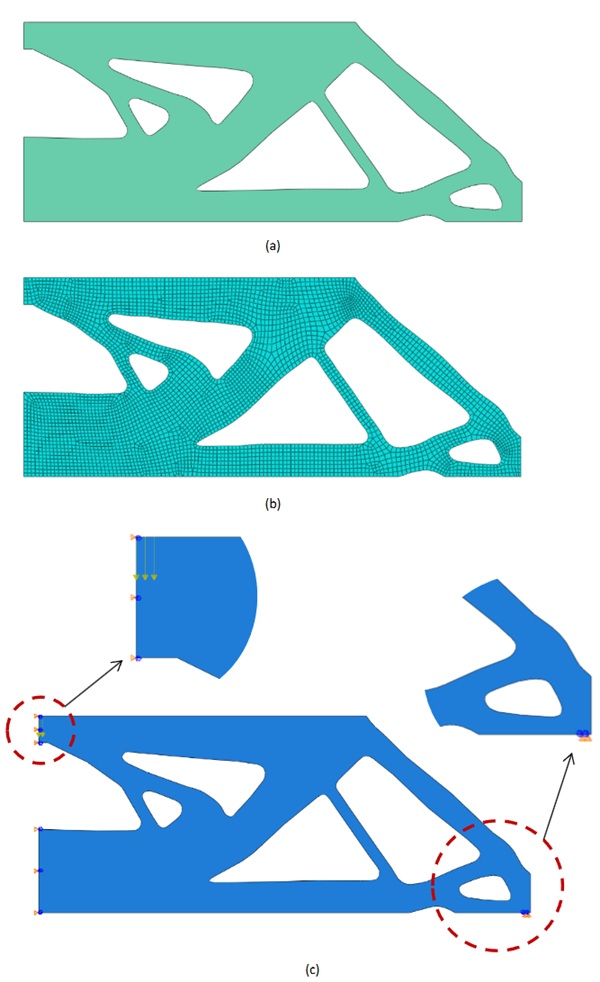
4.2. 3D structure

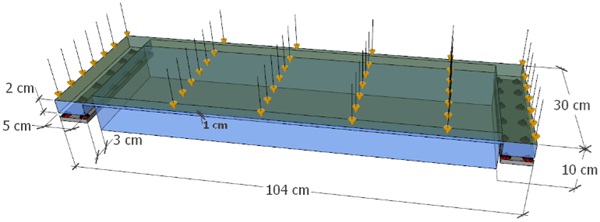
In this section, we perform topology optimization of a 3D stair tread subjected to self-weight load and a uniform load of 3 N/cm² as shown in Fig. 9. The structure is discretized into 23 724 elements with a finite element volume of 1 × 1 × 1 cm³. To reduce computational time, only one-quarter of the structure is optimized as the structure is symmetric. The displacement limit is set to 0.20 mm and the filtering radius is 𝑟𝑚𝑖n=17 mm.

Fig. 10 shows the optimized structure with a minimized volume ratio of 0.26. Fig. 11 illustrates the iteration history of volume ratio, stress, and displacement, respectively. Both stress and displacement constraints are satisfied the limit conditions. The maximum displacement and stress of the optimized structure are 0.20 mm and 13.94 MPa, respectively. These values match the corresponding approximated p-norm values which are 0.20 mm and 13.94 MPa, respectively.

5. Conclusion 

This paper has presented a topology optimization including self-weight load for the structural design of glass under maximum principal stress and displacement design criteria using the SIMP method. This implement topology optimization tool is suitable for practical engineering design. Numerical applications were performed for 2D and 3D structures for we used mechanical material properties specifically characterised on AWJ cut glass. The optimized results combined with a numerical validation of mechanical behaviour show that the proposed algorithm can effectively reduce structural weight and increase load-bearing resistance. These findings had not been reported in the literature for structural glass, in particular, fabricated via AWJ cutting. This supports the benefits of topology optimization as an alternative method to design lightweight glass structures of various structural forms and for a wide range of applications.

Acknowledgements

The work was funded by Cambodia Higher Education Improvement Project (Credit No. 6221-KH) and the financial support of the region of Brittany (France) through the ARED funding scheme (gwerenn-Structures haute résistance en verre structurel). We also thank the Dec3D platform (UAR2025 ScanMAT) for sample fabrication.

References

Andreassen, E., Clausen, A., Schevenels, M., Lazarov, B. S., Sigmund, O.: Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 43, 1–16 (2011) . https://doi.org/10.1007/s00158-010-0594-7 
Ashby, M. F., Jones, D. R. H.: Engineering Materials 2 An Introduction to Microstructures and Processing. In: Elsevier, 4th ed. (2013) . https://doi.org/10.1016/b978-0-  08-096668-7.00012-7 
Belis, J., Louter, C., Nielsen, J. H., Schneider, J.: Part H-52. Architectural Glass. In: J. D. Musgraves, J. Hu, L. Calvez (eds.) Springer Handbook oƒ Glass, pp. 1813. Springer Cham (2019). https://doi.org/https://doi.org/10.1007/978-3-  319-93728-1 
Bendsøe, M. P., Sigmund, O.: Extensions and applications. In: Typology Optimization: Theory, Methods, and Applications, pp. 83. Springer Berlin, Heidelberg (2003) https://doi.org/10.1007/978-3-662-05086-6 
Bergman, B.: On the estimation of the Weibull modulus. J. Mater. Sci. Lett. 3, 689–692 (1984). https://doi.org/10.1007/BF00719924 
Bruyneel, M., Duysinx, P.: Note on topology optimization of continuum structures including self-weight. Struct. Multidiscip. Optim. 29, 245–256 (2005). https://doi.org/10.1007/s00158-004-0484-y 
Chen, A., Cai, K., Zhao, Z. L., Zhou, Y., Xia, L., Xie, Y. M.: Controlling the maximum first principal stress in topology optimization. Struct. Multidiscip. Optim. 63, 327–339 (2021) . https://doi.org/10.1007/s00158-020-02701-5 
Choi, S. W., Oh, B. K., Park, H. S.: Design technology based on resizing method for reduction of costs and carbon dioxide emissions of high-rise buildings. Energy Build. 138, 612–620 (2017). https://doi.org/10.1016/j.enbuild.2016.12.095 Damen, W., Oikonomopoulou, F., Bristogianni, T., Turrin, M.: Topologically optimized cast glass: a new design approach for loadbearing   monolithic   glass   components   of   reduced   annealing   time.   Glas.   Struct.   Eng.   7,   267–291 (2022). https://doi.org/10.1007/s40940-022-00181-1 
Daniella, N.: Topologically Optimised Cast Glass Shell (2020) http://repository.tudelft.nl/ 
Duysinx, P., Bendsoe, M. P.: TOPOLOGY OPTIMIZATION OF CONTINUUM STRUCTURES WITH LOCAL STRESS CONSTRAINTS. Int. J. Numer. Methods Eng. 43, 1453–1478 (1998) . https://doi.org/10.1007/s00158-008-0336-2 
Duysinx, P., Sigmund, O.: New developments in handling stress constraints in optimal material distribution. Am. Inst. Aeronaut. Astronaut. 1501–1509 (1998) https://doi.org/10.2514/6.1998-4906 
Giraldo-Londoño, O., Russ, J. B., Aguiló, M. A., Paulino, G. H.: Limiting the first principal stress in topology optimization: a local and consistent approach. Struct. Multidiscip. Optim. 65, 254 (2022) . https://doi.org/10.1007/s00158-022-03320-y
Guest, J. K., Prévost, J. H., Belytschko, T.: Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int. J. Numer. Methods Eng. 61, 238–254 (2004). https://doi.org/10.1002/nme.1064 Hänig, J., Weller, B.: Load-bearing behaviour of innovative lightweight glass–plastic-composite panels. Glas. Struct. Eng. 5, 83–97 (2020) . https://doi.org/10.1007/s40940-019-00106-5
Hänig, J., Weller, B.: Experimental investigations and numerical simulations of innovative lightweight glass–plastic-composite panels made of thin glass and PMMA. Glas. Struct. Eng. 6, 249–271 (2021). https://doi.org/10.1007/s40940-021-00153-x 
Hänig, J., Weller, B.: Integrated connections for glass–plastic-composite panels: an experimental study under tensile loading at +23, +40 and +60°C and different glass build-ups. Glas. Struct. Eng. 7, 211–229 (2022).    https://doi.org/10.1007/s40940-022-00174-0 
Inamura, C., Stern, M., Lizardo, D., Houk, P., Oxman, N.: Additive Manufacturing of Transparent Glass Structures. 3D Print. Addit. Manuf. 5, 269–283 (2018). https://doi.org/10.1089/3dp.2018.0157 
Klein, J., Stern, M., Franchin, G., Kayser, M., Inamura, C., Dave, S., Weaver, J. C., Houk, P., Colombo, P., Yang, M., Oxman, N.: Additive Manufacturing of Optically Transparent Glass. 3D Print. Addit. Manuf. 2(3), 92–105 (2015).    https://doi.org/10.1089/3dp.2015.0021 
Koopman, D.: The Topology Optimised Glass Bridge (2021) http://repository.tudelft.nl/ 
Kothe, C., Bodenko, A., Nicklisch, F., Louter, C.: Thin glass in façades: Adhesive joints for thin glass composite panels with 3D printed polymer cores. Civ. Eng. Des. 3, 35–42 (2021) . https://doi.org/10.1002/cend.202100010 
Le, C., Norato, J., Bruns, T., Ha, C., Tortorelli, D.: Stress-based topology optimization for continua. Struct. Multidiscip. Optim. 41, 605–620 (2010). https://doi.org/10.1007/s00158-009-0440-y 
Liu, K., Tovar, A.: An efficient 3D topology optimization code written in  Matlab. Struct. Multidiscip. Optim. 50, 1175–1196 (2014). https://doi.org/10.1007/s00158-014-1107-x 
Louter, C., Akilo, M. A., Miri, B., Neeskens, T., Ribeiro Silveira, R., Topcu, Van Der Weijde, I., Zha, C., Bilow, M., Turrin, M., Klein, T., O’Callaghan, J.: Adaptive and composite thin glass concepts for architectural applications. Heron. 63, 199–218 (2018) http://heronjournal.nl/63-12/9.html
Nisar, S., Li, L., Sheikh, M. A.: Laser glass cutting techniques—A review. J. Laser Appl. 25, 1–11 (2013). https://doi.org/10.2351/1.4807895 
París, J., Navarrina, F., Colominas, I., Casteleiro, M.: Topology optimization of continuum structures with local and global stress constraints. Struct. Multidiscip. Optim. 39, 419–437 (2009). https://doi.org/10.1007/s00158-008-0336-2 
Pfarr, D., Louter, C.: Prototyping of digitally manufactured thin glass composite façade panels. Archit. Struct. Constr. 3, 263–273 (2023). https://doi.org/10.1007/s44150-022-00080-7 
Querin, O. M., Victoria, M., Alonso, C., Ansola, R., Martí, P.: Chapter 1- Introduction.  In: B. Guerin (ed.) Topology Design Methods for Structural Optimization, pp. 10. Academic Press, Mathew Deans (2017)
Shitanoki, Y., Bennison, S. J., Koike, Y.: Structural behavior thin glass ionomer laminates with optimized specific strength and stiffness. Compos. Struct. 125, 615–620 (2015). https://doi.org/10.1016/j.compstruct.2015.02.013 
Sigmund, O.: Design of material structures using topology optimization. In: Department of Mechanical Engineering/Solid  Mechanics, Technical University of Denmark, Lyngby, Denmark DCAMM, (1994)
Sigmund, O.: Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 33, 401–424 (2007). https://doi.org/10.1007/s00158-006-0087-x 
Silveira, R. R., Louter, C., Klein, T.: Flexible transparency-A study on Adaptive Thin Glass Façade Panels. Proc. Challenging Glas. 6 (CGC 6) Int. Conf. Archit. Struct. Appl. Glas. 135–148 (2018) . https://doi.org/10.7480/cgc.6.2129 Stefanaki, M. I.: GLASS GIANTS Mass-optimized massive cast glass slab (2020) http://repository.tudelft.nl/ 
Sullivan, J. D., Lauzon, P. H.: Experimental probability estimators for Weibull plots. J. Mater. Sci. Lett. 5, 1245–1247 (1986) . https://doi.org/10.1007/BF01729379 
Svanberg, K.: The method of moving asymptotes—a new method for structural optimization. Int. J. Numer. Methods Eng. 24, 359–373 (1987). https://doi.org/10.1002/nme.1620240207 
Wang, F., Lazarov, B. S., Sigmund, O.: On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 43, 767–784 (2011) . https://doi.org/10.1007/s00158-010-0602-y 
Yoshida, S., Sanglebœuf, J. C., Rouxel, T.: Quantitative evaluation of indentation-induced densification in glass. J. Mater. Res. 20, 3404–3412 (2005). https://doi.org/10.1557/jmr.2005.0418
Zhang, S., Li, H., Huang, Y.: An improved multi-objective topology optimization model based on SIMP method for continuum structures including self-weight. Struct. Multidiscip. Optim. 63, 211–230 (2021) . https://doi.org/10.1007/s00158-020-02685-2