Assessment of different concepts for pre-stressing glass beams with ironbased shape memory alloy elements

This paper was first presented at GPD 2023.

Link to the full GPD 2023 conference book: https://www.gpd.fi/GPD2023_proceedings_book/

Authors:

• Vlad-Alexandru SILVESTRU
• Zhikang DENG
• Andreas TARAS
  Institute of Structural Engineering, ETH, Zurich 

Abstract 

The feasibility of mechanically pre-stressing laminated glass beams with adhesively bonded iron-based shape memory alloy (FeSMA) strips has been assessed in recent experimental investigations. By adding such pre-strained strips along the edges of glass beams, anchoring them to the glass beam ends and activating them, the initial fracture load of the beams can be increased, and especially their post-fracture load-bearing capacity can be significantly improved. This contribution introduces concepts for prestressing laminated glass beams with Fe-SMA tendons adhesively or mechanically connected to the glass beams. These concepts are assessed and compared to each other as well as to non-reinforced laminated glass beams based on finite element analysis results. The models used for simulating the pre-stressing process and the structural performance under four-point bending have been validated with previously conducted experiments. The presented results emphasize the advantages of different concepts and point out identified limitations.

1. Introduction 

Laminated glass beams are used as supporting structural elements for transparent facades or transparent roofs when a maximization of the transparency is aimed. Due to the brittleness of glass and the rather low stiffness of interlayer materials, such beams exhibit a low residual load-bearing capacity after glass fracture. Previous research has shown that both the initial glass fracture load and the residual load-bearing capacity of such beams can be improved by adding ductile tendons and post-tension them (e.g., see [1], [2] and [3]). Despite this, there are few applications of post-tensioned glass beams (e.g. [4]), mostly either (i) because such tendons are considered to be contradictory with the intent of maximizing transparency or (ii) because of the additional complexity of the post-tensioning procedures. However, glass edges are themselves not perceived as transparent and novel materials can allow for less complex post-tensioning procedures. This paper introduces different concepts for post-tensioning laminated glass beams with tendons made of an iron-based shape memory alloy (Fe-SMA) and compares the behaviour of the beams during post-tensioning and under bending load based on finite element (FE) simulations.

The alloy, which exhibits high strength and ductility, has also the property of remembering its initial shape after two phase transformations from austenite to martensite and back (see [5]). The first transformation is obtained by pre-straining and the second one by heating. By fixing pre-strained Fe-SMA strips to a parent structure and triggering the second phase transformation through heating, a pre-stress state can be obtained.

Preliminary investigations on the feasibility of using Fe-SMA strips for post-tensioning glass beams were presented in [6], [7] and [8]. These studies were mainly experimental and focused on adhesively bonded Fe-SMA strips along one or both of the longitudinal glass edges. The studies included activation of the bonded strips by electrical resistive heating and subsequent testing of the post-tensioned glass beams in four-point bending. While using an adhesive joint between the strip and the glass edge is advantageous for obtaining a composite action as well as in terms of crack gaping after glass fracture, the behaviour of the adhesive at high temperatures and over longer durations is a cause of concern. Moreover, adhesive joints represent an issue considering the increasing demand for structural elements to be demountable.

Considering possible loading situations on glass beams, post-tensioning tendons can be positioned either along both longitudinal glass edges resulting in a uniform compressive pre-stress (see Fig. 1a), or along just one of the longitudinal glass edges leading to a precambering (see Fig. 1b). Both of these cases were investigated in this paper

2. Materials and methods 

2.1. Investigated post-tensioned beam concepts

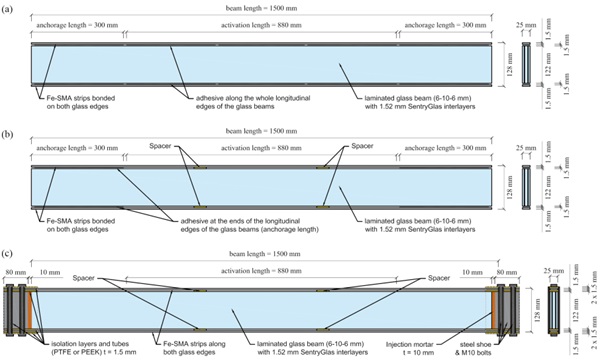
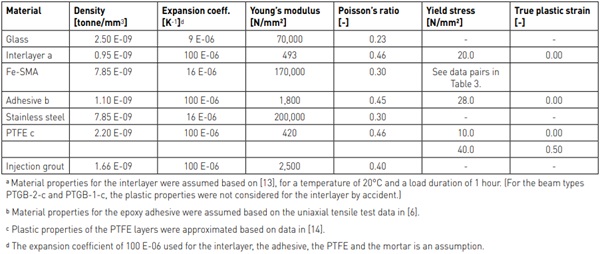
Three different concepts for connecting the Fe-SMA strips to the glass beams were investigated for both cases of two-sided FeSMA strips and one-sided Fe-SMA strips. The dimensions of the (medium-scale) laminated glass beams for this study – with a length of 1500 m, a height of 122 mm and an assembly with three glass layers (6 mm | 10 mm | 6 mm) and 1.52 mm interlayers – as well as the thicknesses of the Fe-SMA strips and the adhesive layers, both with 1.5 mm, were chosen in agreement with the experimentally investigated glass beams in [3] and [7].

The geometries of the three beam types with two-sided Fe-SMA strips and their main components are illustrated in Fig. 2. For the first two types (PTGB-2-a and PTGB-2-b), the Fe-SMA strips were connected to the glass edges by adhesive joints. The difference was that for the first one (PTGB-2-a), the strips were bonded over the whole edge length, while for the second one (PTGB-2-b), they were bonded only over a defined anchorage length at the two ends (determined based on the results in [6]), while there was no adhesive over the activation length in between. The activation length is the length over which the Fe-SMA strips would be heated for activation (posttensioning). This length was kept constant for all investigated beam types. In the case of the third beam type (PTGB-2-c), the Fe-SMA strips were connected mechanically with bolts to stainless steel blocks positioned at the ends of the laminated glass beams. Isolation layers (e.g. PTFE or PEEK) were used between FeSMA strips, bolts and steel block to avoid an undesired electricity flow during an activation by electrical resistive heating (see description of the method in [6]). The pre-stress was introduced to the glass beams through a layer of injection mortar. Spacers made of PTFE were positioned between the glass edges and the Fe-SMA strips in the load axes for the beam types without adhesive at these locations.

For the beam types with one-sided Fe-SMA strips (PTGB-1-a, PTGB-1-b and PTGB-1-c) only that with a mechanically anchored tendon is shown in Fig. 3 (PTGB-1-c). Their geometry and components was similar to that of the beams with two-sided strips, with the only difference that they had Fe-SMA strips only along the bottom glass edge.

2.2. Finite element modelling and simulation approaches 

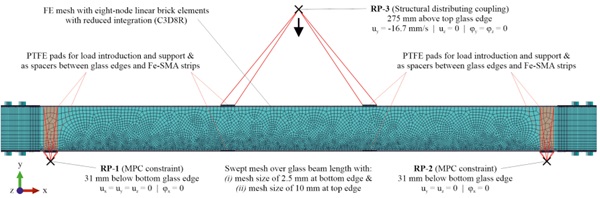
The finite element simulations were conducted with the computer-aided engineering software Abaqus [9] explicit with similar assumptions to those introduced in [10] and [11]. The modelling assumptions were validated by comparing the finite element results with the experimental ones presented in [7]. Detailed results from the validation study will be published in a journal article in the near future. Fig. 4 gives an overview of the model with the density of the finite element mesh and the defined support and loading conditions. All beam types were supported such that the span was 1400 mm in order to allow a good comparison of the results. The simulations included two steps – (i) post-tensioning /activation of the tendons and (ii) four-point bending. The post-tensioning of the beams was modelled with predefined fields by cooling the tendons over the activation length of 880 mm by 90°C. This assumed temperature value was validated based on the tests described in [7]. The load for the four-point bending was applied under displacement control with a speed corresponding to 1 mm/min and a time scaling factor of 1000, which was necessary to allow the simulations to complete in a reasonable amount of time. The distance between the load points was 400 mm. The boundary conditions and the load were applied on reference points, which were connected to PTFE layers used to reduce stress peaks in the load introduction and support areas. Although the simulations were performed non-linear, initial geometric imperfections and potential occurrence of buckling issues were not considered in this study.

All components were meshed with 8-node linear brick elements with reduced integration (C3D8R). The density of the mesh was modelled to be finer along the bottom edge (mesh size of 2.5 mm) and coarser along the top edge (mesh size of 10 mm) for allowing a better capture of the fracture patterns in the glass. The interactions between the glass layers and the interlayers as well as the interactions between the adhesive and both the tendons and the glass edges were modelled as tie constraints, allowing to transfer both tensile and compressive forces. The PTFE layers used in the support and loading areas were tied to the glass and tendon surfaces for reduced computation time and better convergence. Moreover, the isolation layers used to separate the tendons from the steel shoes (blocks) and the injection mortar were tied to the steel shoes, while the isolation tubes for separating the tendons from the bolts were tied to the bolts. For the interactions between the tendons and the glass edges as well as between the injection mortar and the glass edges, properties were defined to allow separation in case of tension. Similar interaction properties were also used for the contact between the isolation layers and the glass, and between the isolation tubes and all touching components on their exterior (tendons, steel shoes, isolation layers).

2.3. Material models 

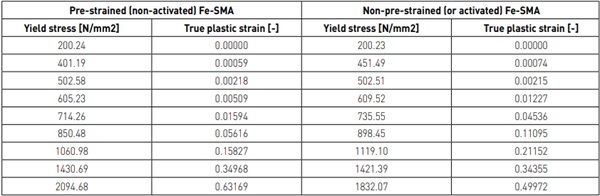
The properties in Table 1 were used for the different materials included in the investigated systems. For the Fe-SMA, the adhesive, the interlayer and the PTFE, plastic properties were defined additionally to the elastic ones for better predicting the residual stiffness of the beams. For the Fe-SMA, the plastic material behaviour in the pre-strained and the activated states was defined as true stress vs. true plastic strain data pairs as given in Table 2. This data was determined with the Ramberg-Osgood model proposed in [12].

In order to simulate the residual load-bearing capacity of the beams, the brittle cracking model available in Abaqus was used to predict the cracking in the glass layers. The necessary parameters were defined based on [10] and [11]. A tensile strength (failure stress) of 45 MPa and a mode I fracture energy of 3 J/m² were defined for the glass in the beam types for which the tendons were not bonded to the glass edges along the activation length. For the beam types PTGB-2-a and PTGB-1-a, a higher failure stress of 70 MPa was chosen based on the strain measurements conducted for the experimentally tested beams of type PTGB-2-a in [7]. This higher possible stresses are attributed to the fact that the adhesive delays the crack initiation and is bridging the cracks impeding them to grow. The behaviour after cracking was described with the “brittle shear” option in Abaqus and the necessary material parameters e = 0.005 and p = 5, which allow to estimate the shear modulus of the cracked glass as a ratio of the shear modulus of the glass without cracks. Furthermore, the “brittle failure” option in Abaqus was used to remove cracked elements from the mesh based on a failure displacement, which depends on the failure stress and the fracture energy. A value of 13.3E-05 mm was used for a failure stress of 45 MPa and of 8.6E-05 mm for a failure stress of 70 MPa.

3. Results and discussion 

3.1. Post-tensioning / Activation of Fe-SMA

The stress distribution in the glass beams after activation of the Fe-SMA tendons (after post-tensioning) was different for the beams with two-sided tendons compared to those with one-sided tendons. For the first ones, an almost uniform compressive stress state was obtained over the whole height of the glass beams, while for the latter ones, compressive stresses resulted along the bottom edge and tensile ones along the top edge (see contour plots in Fig. 5). Moreover, it was noticed that for the beams with tendons adhesively bonded only in the anchorage area, higher local compressive stresses resulted near the inner ends of the adhesive joints, both for the beams with two-sided and those with one-sided tendons. Fig. 5 also shows, that in the case of mechanical anchoring the obtained stress states extended over the whole beam length, while for the beams with adhesive bonding, the stress states extended only over the activation length.

For a quantitative comparison of the results after post-tensioning, stresses in the glass and in the Fe-SMA tendons along with the vertical displacements in the middle of the bottom glass edge are given in Table 3. It was observed that the highest pre-stress was achieved in the case of adhesive bonding along the whole glass edges, while in the case of mechanical anchoring of the tendons, the pre-stress levels were around half as big.

3.2. Four-point bending simulations 

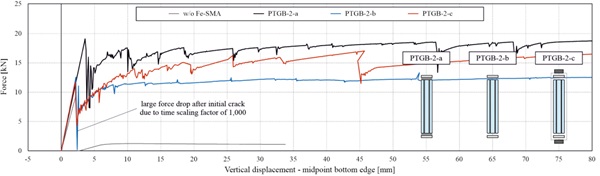
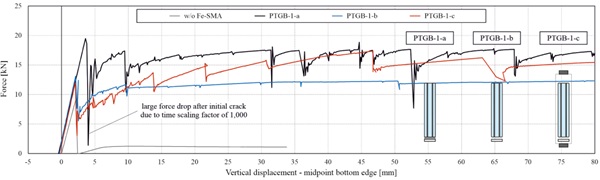
The behaviour of the different beam types in four-point-bending was analysed based on the force vs. vertical displacement curves shown in Fig. 6 for the beams with two-sided tendons and in Fig. 7 for those with one-sided tendons. Additionally, the two diagrams also include the curve for a reference laminated glass beam without any tendons. By comparing the two diagrams, it was observed that the additional tendon along the top edge (compressed edge) did not have a significant influence for the applied load direction. However, the additional tendon would have a relevance for loading in the opposite direction (as it might occur for glass fins in facades) and is expected to also have a positive effect for eventual buckling occurrence. Both for the beams with twosided and those with one-sided tendons, the diagrams show a higher initial crack force as well as a higher residual load-bearing capacity for tendons bonded along the whole beam length. This is mainly because of the assumed higher tensile strength in these cases, based on the experimental measurements conducted in [7]. The beams with mechanically anchored tendons showed slightly lower initial fracture forces compared to those with adhesively bonded tendons in the anchorage area. The higher residual load-bearing capacity of the beams with mechanically anchored tendons needs to be further investigated, since it might be due to the accidentally neglected yielding of the interlayer in these cases.

In addition to the force vs. displacement diagrams, the crack patterns of the middle glass layer for the different beam types are shown in Fig. 8 for the beams with two-sided tendons and in Fig. 9 for those with one-sided tendons (i) after the initial glass fracture and (ii) after a vertical displacement of 60 mm. After initial glass fracture more than one crack is visible due to the chosen output interval for results. After larger displacements, it was observed that the beams with tendons adhesively bonded over the whole length of the longitudinal edges (especially PTGB-1-a) exhibited more distributed cracks than the other ones. The fracture pattern obtained for the beams with mechanically anchored tendons at higher displacements might have been influenced by the neglected yielding of the interlayer and needs to be verified in future investigations. The lateral movement of the steel shoes away from the glass beams in Fig. 9-f is due to the allowed separation between the different components and the assumed supports in the area of the white PTFE layers. These supports were assumed to allow a good comparison between the results for the different beams. However, in reality the steel shoes would be supported as well. Further, the bolts could be pre-stressed in order to avoid such a movement.

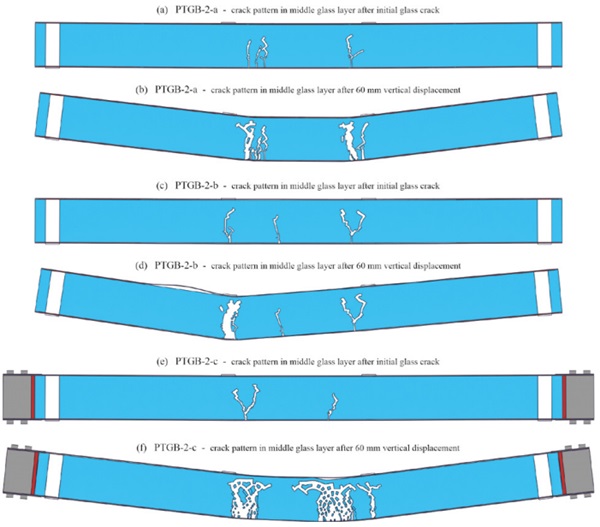
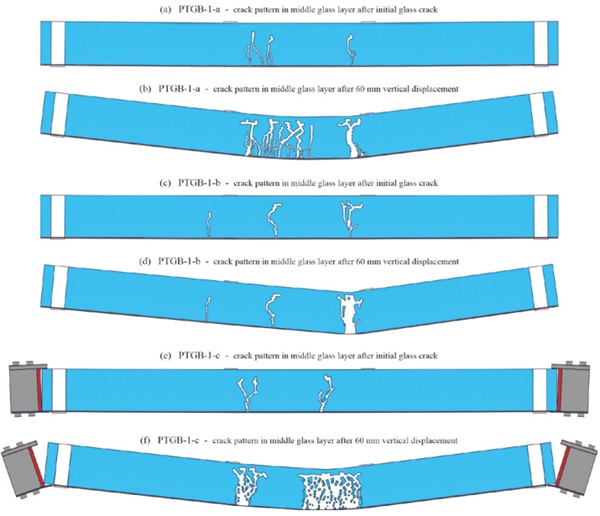
4. Conclusions 

Overall, the obtained results showed that the post-tensioned glass beams with adhesively bonded Fe-SMA tendons along the whole length of the longitudinal glass edges performed best. This depended among others on the material properties used for the adhesive and the higher glass strength assumed based on experimental results. Further, it was observed that the residual load-bearing capacity could also be increased by systems without adhesive bonding, however, less effectively. Future studies should focus on eventual buckling problems of such systems during activation and subsequent loading and should also include experimental validation of the systems without adhesives.

Acknowledgements 

This research was conducted as an extension of the experimental investigations performed within the innovation cheque number 51447.1 INNO-ENG funded by Innosuisse – Swiss Innovation Agency and supported by re-fer AG.

References

[1] K. Martens, R. Caspeele, J. Belis, Development of Reinforced and Posttensioned Glass Beams: Review of Experimental Research, Journal of Structural Engineering 142 (5) (2016) 04015173. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001453.
[2] C. Louter, J. van Heusden, F. Veer, J. Vambersky, H. de Boer, J. Versteegen, Post-Tensioned Glass Beams, presented at the Fracture of Nano and Engineering Materials and Structures, Dordrecht, 2006.
[3] J. Cupać, C. Louter, A. Nussbaumer, Flexural behaviour of post-tensioned glass beams: Experimental and analytical study of three beam typologies, Composite Structures 255 (2021) 112971. https://doi.org/10.1016/j.compstruct.2020.112971.
[4] H. Schober, H. Gerber, J. Schneider, Ein Glashaus für die Therme in Badenweiler, Stahlbau 73 (11) (2004) 886-892. https://doi.org/10.1002/stab.200490213.
[5] M. Shahverdi, J. Michels, C. Czaderski, M. Motavalli, Iron-based shape memory alloy strips for strengthening RC members: Material behavior and characterization, Construction and Building Materials 173 (2018) 586-599. https://doi.org/10.1016/j.conbuildmat.2018.04.057.
[6] V.-A. Silvestru, Z. Deng, J. Michels, L. Li, E. Ghafoori, A. Taras, Application of an iron-based shape memory alloy for post-tensioning glass elements, Glass Structures & Engineering 7 (2) (2022) 187-210. https://doi.org/10.1007/s40940-022-00183-z.
[7] V.-A. Silvestru, Z. Deng, J. Michels, A. Taras, Enabling a Ductile Failure of Laminated Glass Beams with Iron-Based Shape Memory Alloy (FeSMA) Strips, ce/papers 5 (4) (2022) 948-956. https://doi.org/10.1002/cepa.1839.
[8] J. Rocha, E. Pereira, J. Sena-Cruz, Feasibility of mechanical post-tensioning of annealed glass beams by activating externally bonded Fe-SMA reinforcement, Construction and Building Materials 365 (2023) 129953. https://doi.org/10.1016/j.conbuildmat.2022.129953.
[9] Abaqus/CAE 2021. (2020). Dassault Systemes Simulia Corp., Johnston, RI, USA.
[10] C. Bedon, C. Louter, Exploratory numerical analysis of SG-laminated reinforced glass beam experiments, Engineering Structures 75 (2014) 457-468. https://doi.org/10.1016/j.engstruct.2014.06.022.
[11] C. Bedon, C. Louter, Finite Element analysis of post-tensioned SG-laminated glass beams with adhesively bonded steel tendons, Composite Structures 167 (2017) 238-250. https://doi.org/10.1016/j.compstruct.2017.01.086.
[12] V.-A. Silvestru, Z. Deng, A. Taras, On predicting the behaviour of an iron-based shape memory alloy with the Ramberg-Osgood model, ce/papers(2023). submitted for Eurosteel 2023 conference.
[13] Kuraray, Trosifol SentryGlas - Product Portofolio.
https://www.trosifol.com/fileadmin/user_upload/
TROSIFOL/support/downloads/product_brochures/
pdf_documents/sentryglas/SentryGlas_8_2019_
engl_web.pdf (accessed 15.02.2023).
[14] J. L. Jordan, C. R. Siviour, J. R. Foley, E. N. Brown, Compressive properties of extruded polytetrafluoroethylene, Polymer 48 (14) (2007) 4184-4195. https://doi.org/10.1016/j.polymer.2007.05.038.