Experimental tests and numerical simulations of ballistic impact on laminated glass

Authors: Karoline Osnes, Jens Kristian Holmen, Tormod Grue and Tore Børvik

Source: EPJ Web Conf., 250 (2021) 02022 | https://doi.org/10.1051/epjconf/202125002022

Abstract

In this study, we investigate double-laminated glass plates under ballistic impact through experimental tests and numerical simulations. The experimental tests are used to determine the ballistic limit velocity and curve for the laminated glass targets, and to create a basis for comparison with numerical simulations. We tested two different glass pane configurations: (1) one double-laminated glass plate, and (2) two layers of double-laminated glass plates separated by an airgap. In the numerical study, we used finite element simulations that employed higher order elements and 3D node splitting to predict the residual velocities of the bullets in the experiments. Node splitting enabled modelling of fracture by element separation and was employed for the glass parts. The material and fracture models that we used for the glass and the PVB parts were simplified, but the numerical predictions proved to be in excellent agreement with the experimental results. 

1 Introduction

Annealed float glass is widely used in windows, and its mechanical properties are dominated by a highly brittle behaviour. Consequently, such windows will provide limited protection against ballistic impact. However, if the windows are made with multiple layers of glass and polymer, they can serve as bullet resistant. This type of sandwich structure is called laminated glass. When laminated glass is impacted by a projectile and the glass layers fracture, the polymer will retain large glass fragments and prevent them from being ejected from the window. In general, the fracture strength of glass varies considerably and is dependent on factors such as the boundary condition, loading type and rate, and geometry of the plate.

This stochastic fracture behaviour is caused by microscopic flaws, in which fracture typically initiates. For fracture to initiate in these flaws, they must undergo mode I loading (i.e., opening of the flaws). Consequently, glass plates primarily fail in tension [1]. Under ballistic loading, failure mechanisms other than tension failure typically arise. When impacted by a projectile, the glass plate experiences compression and shear loading at high strain rates, which induce fracture and pulverization of the glass material. If the glass plate is relatively thin, the plate may experience tensile failure initiated on the back side. For thick glass plates, however, the tensile strength is considered less crucial to the ballistic performance [2].

In this study, we investigate double-laminated glass panes under ballistic impact by 7.62 mm AP bullets through both experimental tests and numerical simulations. Two different glass pane configurations are tested: (1) one double-laminated glass plate, and (2) two layers of double-laminated glass separated by a 24 mm airgap. In the numerical part of the study, finite element simulations employing higher order elements and 3D node splitting are used to recreate the global behaviour (i.e., perforation resistance) during ballistic impact.

2 Experimental tests

2.1 Laminated glass

The laminated glass plates used in this study consist of three 3.8 mm thick glass plates and two 1.52 mm thick polymer interlayers, resulting in a total thickness of 14.44 mm. The inplane dimensions of the plates are 400 mm × 400 mm. The glass material is annealed sodalime silica float glass, and the polymer is polyvinyl butyral (PVB) of the type Saflex RB-41.  Glass is a brittle material and behaves in a linear-elastic manner to the point of fracture. The fracture strength of glass is probabilistic and is caused by the presence of microscopic surface flaws. These flaws cause glass plates to primarily fail during tensile loading because fracture initiates in the flaws under mode I loading. Furthermore, the fracture strength depends on factors such as boundary conditions, loading type and rate, and geometry of the glass plate [3]. Note that the variance of the fracture strength is typically low under ballistic impact [4]. 

PVB is the most common polymer used in laminated window glass. The material is very flexible, and it can undergo large strains without much permanent deformation. It is nearly incompressible, and its behaviour depends highly on the strain rate and the temperature [5].  

Laminated glass is made from bonding layers of glass and polymer together through a process including heat and pressure in an autoclave. The polymer interlayer will increase the loading resistance of the component and retain glass fragments after the glass fractures.  

In this work, we investigated double-laminated glass plates under ballistic impact. The configuration with one double-laminated glass plate was tested twice (DLx1-1 and DLx1-2) at two different impact velocities. The configuration with two double-laminated glass plates was tested six times (DLx2-1 to DLx2-6) at five different impact velocities. 

2.2 Bullets

In the experimental study, 7.62 mm armour piercing (AP) bullets impacted the laminated glass plates. The bullet consists of a hardened steel core, a lead cap, and a brass jacket and end cap. The total mass of the bullet is 10.5 ± 0.25 g. For more information about the makeup of the bullet, please refer to Børvik et al. [6]. 

2.3 Ballistic impact

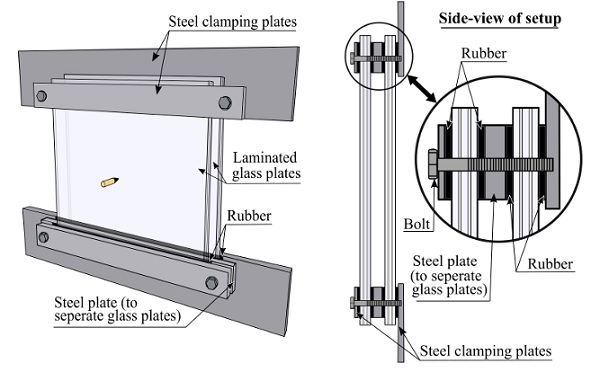
The ballistic impact tests were performed in a ballistic range [6] and the bullets were fired from a smooth-bored Mauser gun with striking velocities between 375 and 700 m/s. The distance between the muzzle and the target plate was approximately 1 m, and the striking point was at the centre of the plate. Fig. 1 shows a sketch of the clamping of the laminated glass plates (for DLx2). Two thick steel beams were used to clamp the plates to the test fixture, and 4 mm rubber strips were placed between the glass and the steel. For the DLx2 tests, the gap between the two double-laminated glass plates was maintained by a 16 mm steel plate and 2 × 4 mm rubber strips. All tests were filmed by a Phantom v2511 high-speed camera with a recording rate of 75,000 fps. The images were later used to find the impact and residual velocity of the bullet by tracing the tip of the bullet. 

2.4 Ballistic results

Table 1 presents the impact (vi) and residual (vr) velocities and pitch angle before impact (αi) for the ballistic impact tests. In DLx2-1 and DLx2-6, the bullet was embedded in the rear plate, while for the remaining tests the bullet retained a residual velocity. Note that the bullet velocities between the two laminated glass plates in DLx2-1 and DLx2-2 can be estimated from DLx1-1 and DLx1-2 since the tests had almost the same impact velocity. 

Table 1. Overview of the ballistic impact tests.

The ballistic limit curves for DLx1 and DLx2 was found by minimising the mean squared error of the Recht-Ipson model [7] to the experimental data, viz.

Here, vbl is the ballistic limit velocity, and a and p are fitting parameters. For DLx1 and DLx2, vbl were calculated as 232.2 m/s and 394.8 m/s, respectively. The fitting parameters a and p were assumed to be equal for DLx1 and DLx2 and were found to be 1.0 and 1.50.  

Fig. 2 shows high-speed camera images from DLx2-2. It is seen that powder-like glass fragments were generated quickly after bullet impact. A short time after contact, the material on the rear plate shattered, presumably due to tensile stresses. Further, we see that the second plate was hit by fragments from the first plate. The lead cap and brass jacket were always peeled off the steel core during impact of the first double-laminated glass plate, while the steel core sustained almost no damage. Similar behaviour was observed in the other tests. For more information regarding the experimental results, please refer to Osnes et al. [8]. 

3 Numerical simulations

3.1 Finite element models

Numerical simulations of the ballistic impact tests were performed using the nonlinear explicit finite element code IMPETUS Afea Solver [9]. The code provides features such as higher order elements and 3D node splitting. Node splitting describes fracture by element separation, while higher order elements provide additional robustness and accuracy.

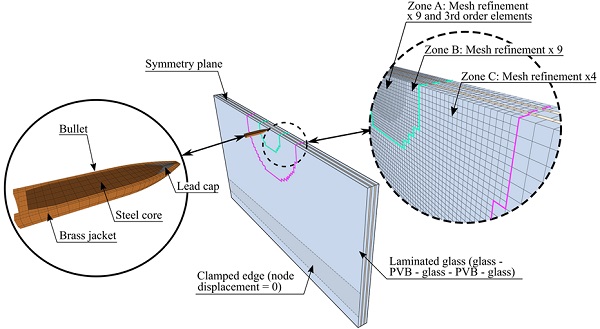
Fig. 3 illustrates the finite element model of DLx1. The model included one symmetry plane and the element size for the glass and the PVB was 2.7 mm × 2.7 mm with one element over the thickness. Three different mesh refinement zones (A, B and C) were included in the plate close to the impact point. The mesh was refined 4 times in zone C, and 9 times in zones A and B. The model consisted mostly of fully integrated 8-node elements. Cubic elements were used in zone A and for the bullet. Node splitting was used to model fracture in the glass. 

3.2 Material models

The glass and the PVB were both modelled as linear elastic materials (defined by Young’s modulus E and Poisson’s ratio ν). Glass fracture initiated when the damage variable Dg 

reached a value of 1. The parameters σs, ts, αs are the fracture stress, fracture time threshold, and fracture initiation exponent, respectively. H is the Heaviside function, which causes fracture to only occur in tension (i.e., when the first principal stress σ1 > 0). Fracture would further propagate when the stress intensity factor KI reached the fracture toughness KIC. For more information, please refer to Osnes et al [10]. To include failure in the PVB, we merely used a critical effective strain criterion 

Note that these models will not capture all local effects occurring during impact (e.g., crushing of glass material). However, the main goal of the simulations was to recreate the global behaviour (i.e., bullet residual velocity), and the contribution from local effects was assumed small. In addition, the glass plates were thin and failure in tension was likely to dominate the global behaviour. 

Table 2 presents parameters used to describe the material and fracture models for the glass and the PVB. The steel core in the bullet was made rigid, while the brass and lead parts were represented by the Johnson-Cook material model and Cockroft-Latham failure criterion, see Holmen et al. [11] for details and the parameter input.  

Table 2. Input parameters for the glass and PVB models. 

3.3 Numerical predictions 

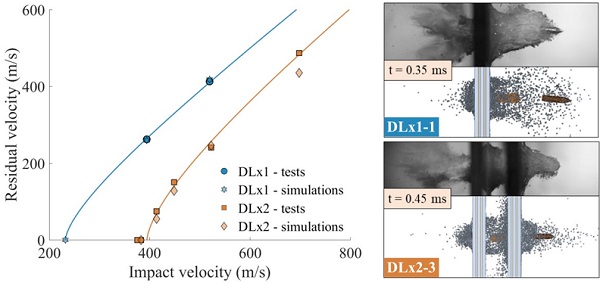
Fig. 4 presents impact versus residual velocities of the experiments and the simulations, including the ballistic limit curves (shown by solid lines). For DLx1, the predicted bullet velocities corresponded extremely well with the experiments (error of 1.2 %). We also ran a simulation of DLx1 with an impact velocity equal to the calculated ballistic limit velocity (232.2 m/s). The simulation resulted in embedment of the bullet in the glass, as we would expect in a physical test. Simulations of DLx2 also showed a good agreement with the experiments, and the simulation of DLx2-1 resulted in embedment of the bullet.

However, the DLx2 simulations provided in general a slightly higher resistance than the experiments, and an error of 10 % was found for the highest impact velocity (vi = 698.3 m/s). On the right side of Fig. 4, images of DLx1-1 and DLx2-3 from the experiments and simulations are compared. The trajectory of the bullet seems to follow the experiments well, and the brass jacket is stripped off during impact of the first plate. The fracture and pulverization of the glass are not entirely captured by the simulation, which is partly due to the coarse mesh of the glass and the simplified material and fracture models for the glass and the PVB. For more information, the reader is referred to Osnes et al. [8]. 

4 Concluding remarks

In this study, we investigated double-laminated glass plates under ballistic impact through experimental tests and finite element simulations. Two different configurations were tested, i.e., a single pane configuration (DLx1) and a double pane configuration (DLx2). DLx1 was tested twice, while DLx2 was tested six times. The bullet was embedded in the rear plate in two of the DLx2 tests, and for the remaining tests, the bullet perforated the plates. The ballistic limit velocities vbl for DLx1 and DLx2 were estimated to be vbl=232.2 m/s and vbl=394.8 m/s, respectively. The material and fracture models used for the PVB and glass in the finite element simulations were simplified. Still, the simulations recreated the global behaviour of the experiments very well. Thus, the numerical framework has a great potential for use in ballistic impact simulations of highly brittle materials such as glass.  

The present work has been carried out with financial support from the Norwegian Defence Estates Agency, the Centre of Advanced Structural Analysis (CASA), Centre for Research-based Innovation, at the Norwegian University of Science and Technology (NTNU) and the Research Council of Norway through project no. 237885 (CASA).

References

1. K. Osnes, T. Børvik, O.S. Hopperstad, Eng. Fract. Mech, 201, 107-129 (2018)
2. X. Zhang, H. Hao, G. Ma, Int. J. Impact Eng., 77, 108-119 (2015)
3. K. Osnes, O.S. Hopperstad, T. Børvik, Eng. Struct., 212, 110516 (2020)
4. C. Jr. Anderson, C. Weiss, S. Chocron, Technical Report No. 18.12544/018, Southwest Research Institute, San Antonio, TX. (2009)  
5. P. Hooper, B. Blackman, J. Dear, J. Mater. Sci. 47, 3564–3576 (2012)
6. T. Børvik, S. Dey, A.H. Clausen, Int. J. Impact Eng., 36, 948-964 (2009)
7. R.F. Recht, T.W. Ipson, J. Appl. Mech., 30, 60-82 (1963)
8. K. Osnes, J.K. Holmen, T. Grue, T. Børvik, Int. J. Impact Eng. (to be published)
9. IMPETUS Afea Solver. Accessed: 2020-12-12. http://www.impetus-afea.com/
10. K. Osnes, J.K. Holmen, O.S. Hopperstad, T. Børvik, Int. J. Impact Eng., 132, 103334 (2019)
11. J.K. Holmen, T. Børvik, O.S. Hopperstad, Eng. Struct., 130, 216-228 (2017) 6