Article Information
- Digital Object Identifier (DOI): 10.47982/cgc.9.504
- Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess.
- Published as part of the peer-reviewed Challenging Glass Conference Proceedings, Volume 9, June 2024, 10.47982/cgc.9
- Editors: Christian Louter, Freek Bos & Jan Belis
- This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
- Copyright © 2024 with the author(s)
Authors:
- Zhufeng Pan - Shanghai Jiao Tong University
- Jian Yang - Shanghai Jiao Tong University
- Xing-er Wang - Shanghai Jiao Tong University
- Gang Li - Henan Zhongbo Glass Co., LTD
- Xianfang Jiang - Henan Zhongbo Glass Co., LTD
Abstract
Scratch-induced surface damage of aged glass elements can lead to strength degradation of glass material and thus threatens the safety of architectural glass. It is of significance to evaluate the mechanical performance of scratched glass elements. In this study, deep close-to-reality scratch is introduced at the centre of the annealed glass plate by a diamond indenter. Coaxial double ring (CDR) test is conducted to evaluate the flexural performance of scratched glass. The test setup is based on EN 1288-5 standard and the specimens are square size for convenience. A total number of 40 glass plates are tested consisting of intact and scratched specimens with two typical loading rates. Test results show that the loading rate will lead to the variation of material strength but will not significantly influence the crack pattern for both intact and scratched glass. To have a thorough understanding of the fracture process of scratched monolithic glass, numerical simulation of CDR test is performed based on the peridynamics (PD) theory. The scratch features in the model are simplified to improve the computational efficiency. Deflection Results obtained from the plate theory are used to validate the PD model. The initiation and propagation of radial cracks along the surface are captured. Such research findings can contribute to the fracture behaviour evaluation of scratched glass elements.
1.Introduction
Glass has been widely used as a building material throughout the history and is frequently seen in building envelopes. It has both good transparent and mechanical performance (Wang et al., 2021). However, the brittle fracture of glass material is still a challenging issue as the mechanical behaviour of a glass element is governed by its surface condition (Datsiou and Overend, 2017; Veer et al., 2009). More precisely, the fracture of an as-received glass product is triggered by the microscopic flaws at glass surface (Shand, 1965). The distribution and the sizes of surface flaws are problematic and researchers have focused on evaluating it using statistical approach for the design of glass elements (Beason and Morgan, 1984; Yankelevsky, 2014). However, such approaches are not suitable for evaluating the mechanical behaviour of aged glass elements as they can undergo severe environment during the service stage and are prone to encounter deep surface damage. Such damage can threaten the safety of the elements.
Scratch-induced damage is one of the most typical surface damage for aged architectural glass elements as they are served to be exposed to the external environment. Scratch has proved to have negative impact on both transparent and mechanical performance of glass material (Swab et al., 2013; Schneider et al., 2012; Bandyopadhyay et al., 2012; Cui et al., 2024). To evaluate the mechanical performance of scratched monolithic glass (Pan et al., 2024), most researchers have concentrated on the mechanical strength degradation of scratched glass by introducing controllable artificial deep close-to-reality scratch by laser-based approaches (Nategh et al., 2021) or a diamond indenter (Pan et al., 2021; Le Houérou et al., 2003). Key scratch features that can influence the glass strength have been investigated. However, it is not enough to only consider its effect towards material strength, fracture behaviour including the fracture initiation and propagation are also important and need to be paid attention to.
To capture the fracture behaviour of scratched monolithic glass, several types of mechanical test have been conducted. Coaxial double ring (CDR) test is one of the most common test setup to determine the flexural strength of brittle material by adding out-of-plane loads through two concentric rings (Castori and Speranzini, 2019). It is hence suitable to investigate the crack pattern of scratched glass under flexural loading. However, the test is hard to capture the whole fracture process of a glass plate even with high-speed camera. Numerical analysis is an effective way to address this issue (Xu et al., 2021; Wang et al., 2022). Mesh-based methods such as finite element (FE) method with cohesive elements have been employed but it is still unsatisfactory on modelling 3D crack propagation. In recent years, a mesh-free method called peridynamics (PD) has attracted much attention as it exhibits convincible performance on modelling 3D crack propagation. It has been applied into modelling the facture behaviour of glass elements and would be suitable for exploring scratch-induced fracture(Naumenko et al., 2022; Jafaraghaei et al., 2022).
In this study, the flexural behaviour of scratched monolithic glass is first investigated by the CDR test. The fracture origin and overall crack pattern influenced by the scratch are obtained. A precise 3D numerical model considering the simplified scratch geometry is established and the fracture behaviour of scratched glass is investigated through a peridynamics analysis.
2. CDR test
2.1. Glass specimens
In this study, soda lime silica (SLS) glass specimens are square shape with the thickness of 3 mm and the size of 100×100 mm. The specimens are provided by Henan Zhongbo Glass Co., Ltd to guarantee a consistent surface condition. All glass specimens are annealed (AN) glass. Air side and tin side of each specimen is distinguished by the UV light inspection. Surface damage is introduced by a tailor-made scratch testing machine, as Fig.1 illustrates. It can generate deep close-to-reality artificial scratch damage by applying normal scratch load with a constant moving speed of 5 mm/s. Indenter is in spherical shape with a diamond tip which has the angle of 120° and the radius of 0.1 mm. The applied load level is set as 20 N. All scratches are 10 mm long and are placed on the tin side of the specimen which is normally exposed to the external environment and is more likely to have critical scratch-induced surface damage.

2.2. Test setup
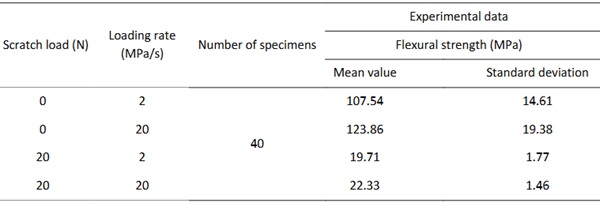
The CDR test is employed to obtain the crack pattern of both intact and scratched monolithic glass plate under flexural loading according to the European standard EN 1288-5. The diameter of the loading ring and the reaction ring are 18 mm and 90 mm, respectively, as shown in Fig. 2. Test was conducted on a universal testing machine with a 10 kN load cell. A 0.06 mm thick self-adhesive film was used to hold the fragments together for fractographic analysis of fracture origin and crack pattern after failure. To investigate the effect of loading rate on both flexural strength and crack pattern of the intact glass and the scratched glass, two typical stress rate were employed in the test. Tests of both 2 MPa/s and 20 MPa/s were conducted. The corresponding displacement rate of the test were 0.013 and 0.13 mm/s, respectively. Each series consists ten specimens to guarantee the reliability. A total number of 40 specimens were tested. Flexural Load added by the universal testing machine and the central deflection of the glass specimens were recorded during the tests.
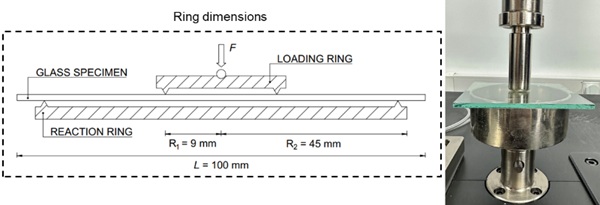
2.3. Test results
The equibiaxial flexural strength of glass specimens can be calculated based on the Kirchhoff-Love plate theory (Timoshenko and Woinowsky-Krieger, 1959) as the following equation shows:
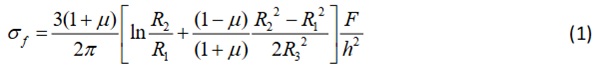
where 𝜎𝑓 is the failure stress, h is the thickness of glass specimen, F is the load at failure, μ=0.23 is the Poisson’s ratio. 𝑅₁ and 𝑅₂ are the radius of the loading and reaction ring, respectively. 𝑅₃ represents the radius of the circular specimen. For square specimen, 𝑅₃ can be calculated from Equation 2, where L is the edge length of the specimen

Test results of the glass specimens are shown in Table.1. The variation of the flexural strength of intact glass is higher than the scratched glass as expected. The fracture of scratched glass occurs prior to the intact specimens.
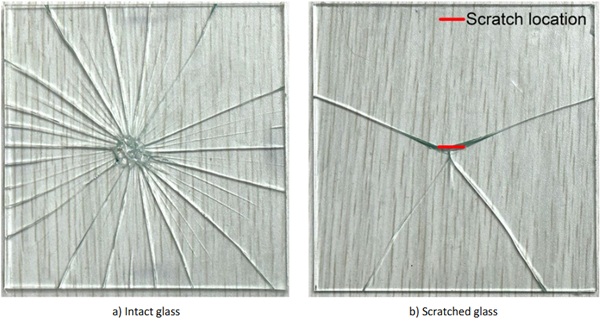
The overall crack pattern of both intact glass and scratched glass are shown in Fig.3. It can be observed that the fracture of scratched glass initiates at a certain point of scratch and only radial macroscopic cracks are found. Meanwhile, more radial cracks and circumferential cracks are found for intact specimens. The fracture initiates inside the loading ring where the maximum principal stress locates. Besides, the crack pattern of intact glass is not influenced by the loading rate, only the flexural strength matters. With the increase of loading rate, the flexural strength of both intact and scratched glass see a slight increase.
Table 1: Test results of coaxial double ring test.
3. Numerical analysis
3.1. Peridynamics theory
PD is a nonlocal form of continuum mechanics, the equilibrium equation is expressed in an integral form, as equation 3 shows
![]()
Where ρ is the material density, u is the displacement vector, 𝑉𝑝 denotes the volume of a point, b(x, t) is the body force vector and the integral domain 𝐻𝑥 is called the horizon at the centre point x and the range of the horizon is denoted as δ.
In PD theory, the fracture of the material is controlled by the breakage of the connecting bonds between the material points. Once a bond breaks, it can no longer carry force so this is an irreversible process. The critical extension of a bond is called the critical bond stretch and it can be related to the critical energy release rate of a material (Silling and Bobaru, 2005) as the following equation shows
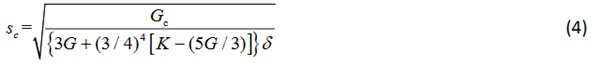
Where 𝐺𝑐 is defined as the critical energy release rate of a material. K and G are bulk modulus and shear modulus, respectively.
3.2. Model setup
The scratch geometry was first introduced to the numerical model through a pre-processing approach to improve the computational efficiency. The basis of this approach is based on the CDR test results. When a scratched glass element is subjected to mode Ι fracture, the linear elastic fracture mechanics theory is suitable to describe the relationship between the critical stress and the scratch depth as follows
![]()
where 𝜎ₙ is the far field stress normal to the crack, a is the depth of a surface damage and Y is the geometry factor which is related to the scratch geometry. Fracture will start when 𝐾=𝐾ΙC and 𝐾ΙC is defined as the fracture toughness of a material. Therefore, the calculation of 𝐾ΙC is as follows
![]()
Where 𝜎𝑠 is the critical stress and 𝑎c is the critical depth of scratch in our study. 𝐾ΙC is 0.75 MPa.√m for soda lime silica glass. The geometry factor of a surface crack is 1.12 (Haldimann et al., 2008). Based on the flexural strength of scratched glass obtained from the CDR test, the critical scratch depth 𝑎c of the AN glass in our study is determined to be 300 μm.
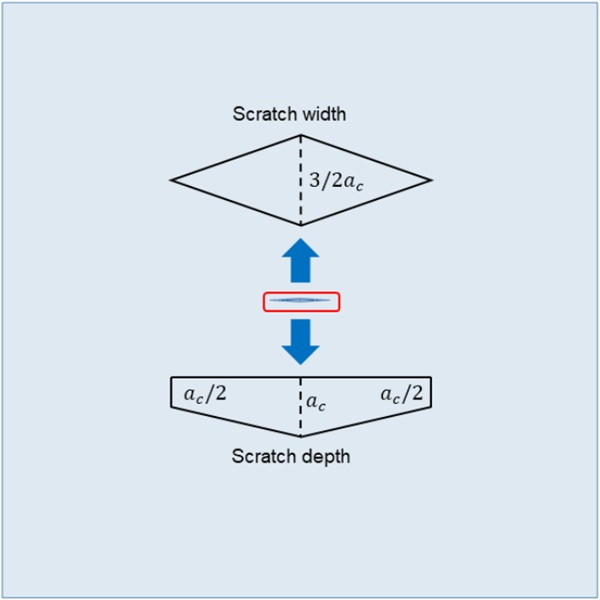
The scratch depth is idealized in our study since the scratch geometry is complex in reality. The maximum scratch depth is defined at the centre of the scratch as the scratching speed is the fastest here and it gradually moves to the end of the scratch for half of the maximum scratch depth. The maximum scratch width is 1.5 times of the maximum scratch depth based on the characterization results from the confocal microscope. The location also lies at the centre of the scratch and the scratch width at the end of the scratch is assumed to be zero. The idealized scratch geometry is built based on these feature points and is inserted into the geometry model of the glass plate, as shown in Fig.4. In our study, glass is modelled as a linear elastic material, with the elastic modulus of 70 GPa and the Poisson’s ratio of 0.23. The type of linear elastic isotropic solid material is selected for our model. A reference FE model is established at first and the model is discretized at the centroid of the element to generate PD model. The element size of the FE model is 0.2 mm and it means that there are 15 layers of material points across the thickness of the plate for PD model. The horizon of the PD model is determined to be three times of the element size after the mesh sensitivity study. The stress rate for the numerical simulation is 20 MPa/s and an explicit solver is used in this study.
3.3. Modelling results
The model is validated by the CDR test and the Kirchhoff-Love plate theory, the central deflection arefound to have negligible difference at the time of 2 s. Then the crack initiation and propagation are investigated based on the validated numerical model. The fracture process of the scratched glass is shown in Fig.5. The fracture process can be clearly presented through the numerical model. The damage is initiated from the maximum depth area at the centre of the scratch and the damage quickly accumulates around the scratch length as the load increases. Crack forms as the damage accumulates and starts to propagate through the whole specimen radially outside the loading ring. The final crack pattern at the time of 1.5 s is close to the observation from the CDR test, showing that the simplification of the scratch geometry is reliable. The crack pattern of scratched glass is completely different with the intact specimen (Naumenko et al., 2022). It is simple comparing with the fracture of intact specimen, indicating that the fracture energy released by the scratched glass is far less than the intact glass. Major type of crack is radial crack and crack branches occur during crack propagation inside the loading ring.

4. Conclusion
In this study, CDR test was first conducted to evaluate the flexural behaviour of the scratched monolithic glass using two small concentric rings, the crack pattern of scratched specimens were captured. As it is observed that the crack pattern of scratched monolithic glass is different from the intact specimens, fracture behaviour of scratched glass is then investigated using peridynamics theory. Several key findings in this study are as follows:
a. The crack pattern of scratched glass is simple comparing with the intact glass specimen as less circumferential and radial cracks appears. It shows that the surface scratch can lead to lower fracture energy release apart from severe strength degradation.
b. The validated peridynamics model is capable of modelling the fracture initiation and propagation induced by the scratch, the fracture is found to initiate at the centre of the scratch with maximum scratch depth. The overall crack pattern is close to the result obtained from the CDR test.
c. The simplified scratch geometry is able to represent complex scratch features and can be inserted into the numerical model to further investigate the effect of key scratch features towards the mechanical behaviour of the monolithic glass.
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Acknowledgements
This work was supported by the National Natural Science Foundation of China [Grant No. 52078293]. The authors also thank the Henan Zhongbo Glass Co., Ltd. for supplying testing materials.
References
Bandyopadhyay, P., Dey, A., Roy, S., & Mukhopadhyay, A. K.: Effect of load in scratch experiments on soda lime silica glass. Journal of Non-Crystalline solids, 358(8), 1091-1103 (2012).
Beason, W. L., & Morgan, J. R.: Glass failure prediction model. Journal of Structural Engineering, 110(2), 197-212 (1984).
Castori, G., & Speranzini, E.: Fracture strength prediction of float glass: The coaxial double ring test method. Construction and Building Materials, 225, 1064-1076 (2019).
Cui, Y., Lam, N., Shi, S., Lu, G., Gad, E., & Zhang, L.: Deterministic failure prediction of toughened glass when impacted by ice. International Journal of Impact Engineering, 185, 104833 (2024).
Datsiou, K. C., & Overend, M.: Artificial ageing of glass with sand abrasion. Construction and Building Materials, 142, 536-551 (2017). https://doi.org/10.1016/j.conbuildmat.2017.03.094
Haldimann, M., Luible, A., & Overend, M. Structural use of glass. IABSE. (2008)
Jafaraghaei, Y., Yu, T., & Bui, T. Q.: Peridynamics simulation of impact failure in glass plates. Theoretical and Applied Fracture Mechanics, 121, 103424 (2022).
Le Houérou, V., Sangleboeuf, J. C., Dériano, S., Rouxel, T., & Duisit, G.: Surface damage of soda–lime–silica glasses: indentation scratch behavior. Journal of Non-Crystalline Solids, 316(1), 54-63 (2003).
Nategh, S., Missinne, J., Vijverman, P., Van Steenberge, G., & Belis, J.: Effect of ultrashort laser-induced surface flaws on architectural glass strength. Construction and Building Materials, 295, 123590 (2021).
Naumenko, K., Pander, M., & Würkner, M.: Damage patterns in float glass plates: Experiments and peridynamics analysis. Theoretical and Applied Fracture Mechanics, 118, 103264 (2022).
Pan, Z., Yang, J., Wang, X.-e., Wang, F., Azim, I., & Wang, C.: Image-based surface scratch detection on architectural glass panels using deep learning approach. Construction and Building Materials, 282, 122717 (2021).
Pan, Z., Yang, J., Wang, X.-e., Zhao, C., Wang, Y., & Zhu, Y.: Assessment on flexural performance of monolithic glass considering spatial and depth characteristics of scratches. Engineering Fracture Mechanics, 109964 (2024).
Schneider, J., Schula, S., & Weinhold, W.: Characterisation of the scratch resistance of annealed and tempered architectural glass. Thin Solid Films, 520(12), 4190-4198 (2012).
Shand, E. B.: Strength of glass—the Griffith method revised. Journal of the American Ceramic Society, 48(1), 43-49 (1965).
Silling, S. A., & Bobaru, F.: Peridynamic modeling of membranes and fibers. International Journal of Non-Linear Mechanics, 40(2-3), 395-409 (2005).
Swab, J., Thies, S., Wright, J., Schoenstein, J., & Patel, P.: Influence of surface scratches on the flexure strength of soda-lime silicate and borosilicate glass. Experimental Mechanics, 53(1), 91-96 (2013).
Timoshenko, S., & Woinowsky-Krieger, S. Theory of plates and shells. McGraw-hill New York. (1959)
Veer, F., Louter, P. C., & Bos, F.: The strength of annealed, heat‐strengthened and fully tempered float glass. Fatigue & Fracture of Engineering Materials & Structures, 32(1), 18-25 (2009).
Wang, X.-E., Meng, Y., Yang, J., Huang, X., Wang, F., & Xu, H.: Optimal kernel extreme learning machine model for predicting the fracture state and impact response of laminated glass panels. Thin-Walled Structures, 162, 107541 (2021). Wang, X.-E., Yang, J., Huang, X., Wang, F., & Zhu, Y.: Voronoi-FDEM concept for modelling post-fracture response of progressively damaged structural glass. Engineering with Computers, 1-14 (2022).
Xu, H., Wang, C. C., Shen, X., & Zlatanova, S.: 3D tree reconstruction in support of urban microclimate simulation: A comprehensive literature review. Buildings, 11(9), 417 (2021).
Yankelevsky, D. Z.: Strength prediction of annealed glass plates–A new model. Engineering structures, 79, 244-255 (2014).