Article Information
- Digital Object Identifier (DOI): 10.47982/cgc.9. 519
- Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess.
- Published as part of the peer-reviewed Challenging Glass Conference Proceedings, Volume 9, June 2024, 10.47982/cgc.9
- Editors: Christian Louter, Freek Bos & Jan Belis
- This work is licensed under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.
- Copyright © 2024 with the author(s)
Authors:
- Nathalie Nießer - Universität der Bundeswehr München
- Geralt Siebert
Abstract
Recently, increased efforts have been made to explore the possibility of using glass panes as structural components, such as shear stiffeners. However, there are obstacles to the widespread use of these panes, even though they have proven their load-bearing capacity in structural systems (Haese 2013). The sudden failure of individual glass panes is a major concern because it can affect the overall structural safety. To better understand the causes of this unpredictable behaviour of glass façades, a numerical and physical sensor concept in the form of a hybrid digital twin will be developed. This involves both measurements of real load-bearing systems and simulations using numerical sensors. The two concepts will initially be developed independently, whereby the virtual model is approximated in a continuous process using measurements of the real structure. For this idea of the hybrid digital twin, a numerical sensor model is first presented in this article, which is also used for the evaluation of real sensors and thus serves as a basis for further investigation. The research project on the safety of glass façades in load-bearing structures is an important step towards improving the reliability and durability of such structures. The introduction of a hybrid digital twin will contribute to the development of an improved safety concept and the further establishment of these applications.
1.Introduction
The construction industry is facing challenges such as time constraints, cost pressures, and increasing technical requirements that lead to higher damage costs, which are often interpreted as indicators of loss of quality (Böhmer et al. 2022). However, it is a matter of definition whether this already constitutes increased building damage. Therefore, this study refers to the definition according to Farrar and Worden (2007), in which a construction defect is defined as any change to a system that affects its material or geometric properties so that its performance is impaired. A direct comparison with the pre-damage condition is required to determine the extent of impairment.
Despite rising refurbishment costs, the total number of reported claims in the German construction industry remained constant between 2016 and 2020 according to an analysis by Böhmer et al. (2022). Furthermore, the analysis of the causes of damage shows that a limited number of factors are responsible for the majority of the damage, with approximately 90% of cases attributable to five main causes: lack of construction management, inadequate execution planning, neglect of protective measures, problems with communication at the interface, and execution or assembly errors. In the civil engineering sector, damage analyses show that structural defects represent the largest proportion, with façades and windows identified as the main weak points, accounting for approximately 43% of the damage cases. These findings underline the need for improved execution quality and more efficient interface coordination and confirm the recurrence of certain types and causes of damage.
This observation is particularly critical for high-risk structures, and also applies to glass façades, whose use can go beyond purely aesthetic aspects, as research has shown that they can perform important structural functions, including horizontal bracing of buildings. It has also been proven that glazing can take on additional load-bearing functions, resulting in lighter and more cost-effective construction. (Haese 2013). This finding is particularly relevant for the development of timber structures, which traditionally have low stiffening potential but can provide significant thermal and structural benefits when combined with glass (Fadai and Winter 2014). However, horizontal loads such as wind or earthquakes are often underestimated during the planning phase, which can lead to considerable damage to the building bracing (Hochhauser 2011).
On the one side, glass façades offer the opportunity for advanced construction, but on the other side, they present an increased safety risk if not designed properly. It is therefore important to recognize construction errors or damage in good time to avoid major failures in critical building structures. (Böhmer et al. 2022). Monitoring of such constructions is therefore essential. This can take many forms, from direct observations to automated data collection. The main objective is to gather and analyse information about the behaviour of a particular system to better understand the various processes that can lead to damage. Modern technologies offer a wide range of options for monitoring structural integrity, especially for the early detection and assessment of structural damage (Zurawski 2015). This is particularly important for the construction of glass façades.
Monitoring with sensor technology ranges from the measurement of deformations, temperatures, humidity levels, and other factors to the detection of deviations from the characteristic movement patterns using acceleration sensors. It is also possible to monitor the quality of materials and components, as well as the ageing processes caused by mechanical or energetic influences (Krawtschuk et al. 2012).
Therefore, Chapter 2.1 deals with the complexity of selecting appropriate sensor hardware for monitoring tasks. The criteria and considerations for sound decision-making and a specific example of glass façade monitoring are presented here. Based on empirical data from sensor measurements, a more precise evaluation and optimization of real sensor performance can be achieved by integrating statistical methods, algorithms, and deep learning models into the monitoring process. The development of such numerical sensors is discussed in Chapter 2.2. Furthermore, both sensor typescan support the development of a hybrid digital twin, which can be seen in Chapter 2,3. After these definitions, Chapter 3 presents the results of a case study in which a proposal is made for a numerical sensor that could be used for monitoring load-bearing glass façades. Whether the use of such numerical sensors can support the planning and optimization of real sensors for building monitoring on load-bearing glass façades is discussed in Chapter 4. In particular, the advantages of numerical sensors for monitoring such structures are highlighted. Finally, the findings of this work are summarized in Chapter 5.
2. Methodology for Digital Twinning
Structural monitoring is a comprehensive concept that includes both technology and methodology. It is important to note that the term 'monitoring' should not be confused with 'control'. Safety is not automatically achieved by the mere implementation of sensors. Rather, safety is the desired state, with monitoring serving as a tool for achieving this goal. Therefore, monitoring provides detailed insight into the specific behaviour of a system. By collecting data, which are then systematically categorized and analysed, valid safety concepts can be developed (Zurawski, 2015).
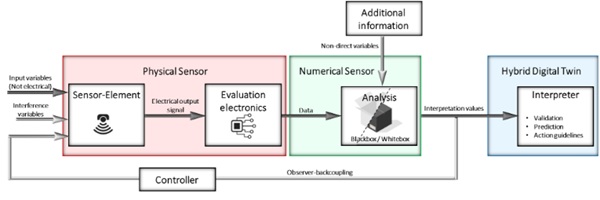
The following discussion focuses exclusively on sensor technology that can be used for monitoring systems and evaluates its effectiveness and importance for the development of a digital twin for glass façades. The steps required to generate a numerical sensor from the hardware component of a sensor, i.e. a physical sensor, and thus create a hybrid digital twin are shown in Figure 1 and are explained in detail in the upcoming sections.
2.1. Physical Sensor
Generally, a sensor is used to record both quantitative and qualitative measurements of physical, chemical, climatic, biological, and medical parameters. The sensor element converts nonelectrical input variables (e.g. temperature or pressure) into electrical output signals. These signals are further processed by signal-processing electronics to generate a sensor signal that is used for control or analysis (Homberg et al. 2023; Hering 2012). The measurement process of the sensor is included in Fig.2 in the red section.
Conducting significant measurements on structures using physical sensors requires careful selection and positioning of the sensors, which is fundamental for the validity of the measurement results (Becker et al. 2014). First, existing damage to structural integrity must be identified, and hypotheses about its causes and possible damage progression must be formulated. This can be done, e.g., through inspections and mapping of the damage or initial measurements on the building. Only then can a suitable sensor concept be developed for long-term measurements and the sensors can be placed at critical points. The ultimate goal of this customized measurement concept is to confirm the occurrence or propagation of damage using measurements, thus enabling preventive measures to be taken against further damage (Farrar and Worden 2007).
2.2. Numerical Sensor
Advances in information technology are crucial for the development of modern surveillance systems. These technologies have enabled new ways of collecting, analysing, and using data on a large scale, and have fundamentally changed the way information is processed. In the context of increasing digitization and advanced data processing, the concept of big data has emerged and become indispensable for modern surveillance systems. Data serve as the basic raw material for all evaluation processes (Zurawski 2015 and Tomažic 2023).
In the last three decades, scientists and researchers have begun to develop predictive models based on physically collected datasets. These models are called numerical sensors (Fig. 2, green section) andrepresent software-based systems that can provide information equivalent to their physical counterparts but are free from the environmental limitations of conventional sensor measurements (Fortuna et al. 2007, Kadlec et al. 2009 and Maier et al. 2021). Such a numerical sensor is characterized by considerably greater flexibility of use. It independently and autonomously generates an output signal based on the combination and aggregation of input data from the physical sensors. The causal relationships between the input and output variables are established by a process-specific model, which necessarily relies on current process information and therefore constantly requires new data (Homberg et al. 2023 and Stebner et al. 2022).
Process models that are suitable for numerical sensors can be divided into two analysis methods. The first category generates secondary variables, which do not require direct process knowledge. These data-driven models, also known as black-box models, are based on comparisons and correlations between the input and output variables. According to Yuan et al. (2020), a number of these models have already been successfully established for soft-sensor applications, including Principal Component Analysis (PCA), Partial Least Squares (PLS), Support Vector Machine (SVM), and Artificial Neural Networks (ANN). In particular, ANNs have proven to be extremely versatile tools for modelling complex, nonlinear systems. This method can be used to build a virtual network from a wide variety of input data, which can approximate almost any causally related technical system. ANNs undergo a learning phase in which their parameters are identified by internal or external information. During this phase, information is passed through the network and adjustments in the structure and parameterization of the network occur through feedback loops. This allows the different decision paths of the network to be trained in specific cases, where connections can be modified and neurons can be adapted (Becker 2010).
Although the implementation of purely data-driven approaches is methodologically simple and does not require process expertise, there is a high risk of approximation and overfitting. This is because reliable investigation of the underlying physical relationships is suppressed. As system knowledge increases, the transition from purely data-driven approaches to model-based methods becomes advantageous. Model-based approaches, also known as white-box models, incorporate this knowledge of the process into the modelling strategy. These models often use fundamental physical equations to establish relationships between measurement and process variables to build information systems (Becker 2010).
2.3. Hybrid Digital Twin
In addition, observers can represent a special form of numerical sensors, which complements the numeric model with a mathematical model of the physical sensors. These models use differential equations to provide feedback between the measured and process variables. They are mainly used when basic knowledge of physical behaviour is available. This correction step leads to a continuous adaptation of the observed variables to the current process state to asymptotically stabilize the observer error (Homberg et al. 2023).
The interaction between empirically collected data, which exhibit extensive, high-dimensional relationships, non-linearities, and redundancies, and numerical models, which aim to capture and simulate these complex real-world processes, form the basis for the development of a hybrid digital twin, Fig. 2, blue section. This connection can independently generate measurements that predict the structural behaviour of systems, and thus enable recommendations for action. In addition, physical sensors can be continuously validated by a digital twin by comparing the predicted sensor measurements with the actual measurements.
3. Results
Once glazing contributes to building bracing, it becomes a critical safety element. Homberg et al (2023) emphasise the need for redundant structures in such systems to minimise the risk of total failure. However, the implementation of redundancy in glazing systems is challenging. The reasons for this can be the complexity of the glass façade technology and the associated maintenance. Specific knowledge is essential for identifying and solving problems. Additionally, the brittleness of glass creates the riskof sudden breakage without warning. Nevertheless, a form of analytical redundancy can be achieved using numerical sensors, which allows both measurable and immeasurable process variables to be estimated (Homberg et al. 2023). These sensors record the load-bearing conditions in glazing and can, therefore, identify redundancies by comparing them with a digital twin. In addition, numerical sensors offer advantages in situations in which direct measurements are not feasible, a sensor fails, or the cost of direct measurements is prohibitive.
In the following study, the feasibility of using numerical sensors for load-bearing glass panes is investigated to provide the first basis for a virtual prediction model.
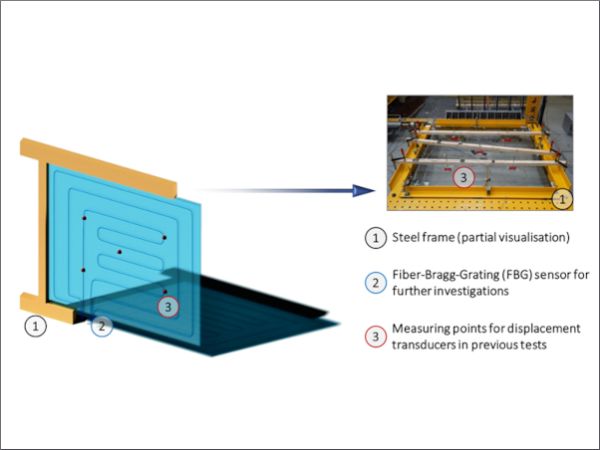
In an experimental setup to investigate the load-bearing behaviour of stiffening glazing (Fig. 2), as performed by Neumer (2018) under laboratory conditions, a composite element consisting of a steel frame, which should correspond to hinged frame corners, and an 8 mm thick monolithic pane of single-pane safety glass is subjected to a load test parallel to the pane. The glass used in this test was linearly supported at all edges. The load was applied using a hydraulic cylinder acting on the corner point of the frame. The glazing deformation was recorded orthogonally at selected points using displacement transducers. Glazing failure was detected at a load of approximately 44 kN when it jumped out of the steel frame.
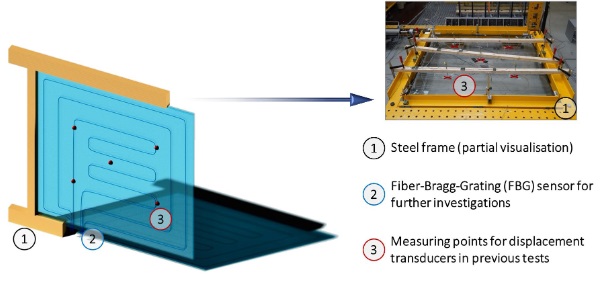
However, this experimental setup can be used only for one-off measurements under laboratory conditions. The aim is to adapt this experiment to long-term measurements of real glass façades in a natural environment. This requires a more robust sensor network to record the deformation of glass panes. Therefore, conventional displacement transducers should be replaced by Fibre-Bragg-Grating sensors integrated into glazing. The possible positioning of these fibre-optic sensors is shown schematically in Fig. 2. Because the function of the sensors in this concept must be maintained consistently over a long period of time, the inspection and verification of the sensor quality is of great importance. It is proposed to complement the measurement data from physical sensors with a numerical sensor concept based on the findings of previous experiments and adapted on an ongoing basis.
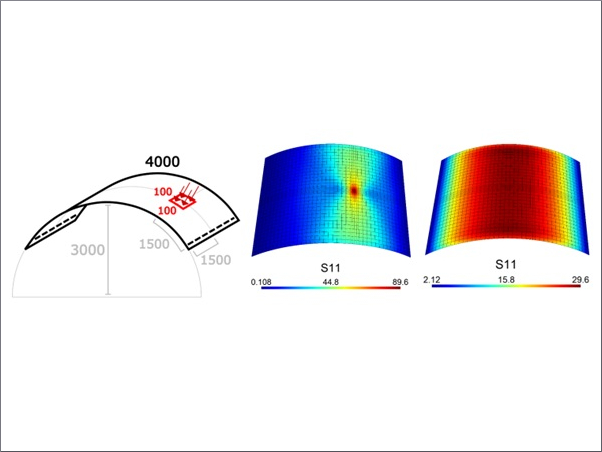
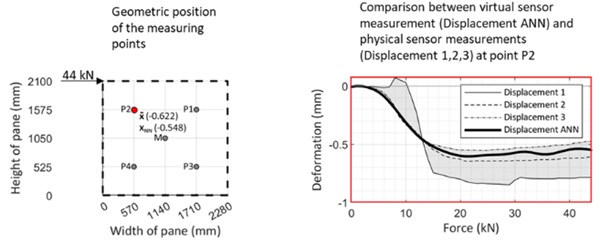
In this case study, based on the test setups shown in Figs. 2 and 3, an ANN was used to train the simulation of the deformation behaviour at point P2 using the input data from points P1, P3, P4, and M. The influence of the spatial coordinates of the measurement points was considered. However, other physical conditions were not included in the black-box analysis. The maximum deformation value calculated using ANN at measurement point P2 with a load of 44 kN was 0.548 mm. This was compared with the measured average deformation value of 0.622 mm. The measured and simulated deformation values are presented in Fig. 3, which shows the convergence of the simulated output data with the measured input data.
According to Backhaus et al. (2015), the ANN used to determine the deformations at measurement point P2 can be described as follows.
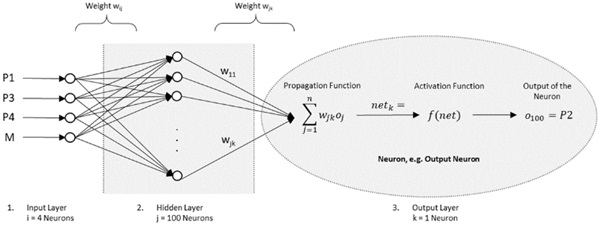
In general, a network consists of neurons that receive signals from pre-connected neurons which areprocessing many incoming signals and weight them according to their association with a single input value. Neurons are organized in a network; in this case, a feed-forward network was used wereneurons are arranged in layers, with information being processed strictly from the input layer to the output layer.
Figure 4 shows the structure of the applied two-layer neural network, where the first layer forms an input layer with four neurons (P1, P3, P4, and M). This layer receives information from the measurements as well as the positions of the measuring points and forwards it to the following layers of neurons. However, the input layers are not counted. Neurons 5 to 100 represent the hidden layer, in which the signals of the upstream neurons are aggregated and nonlinear transformations are performed. This allows the network to represent nonlinear relationships between the input and output values. Neuron P2 provides an output layer that models the independent variables.
To make the training process of a neural network transparent, it is useful to take a closer look at a specific neuron - the output neuron, for example (Fig. 4). Neural networks are characterized by the fact that the internal hidden layers that process input data do not require fixed relationships or theoretical assumptions. The network learns autonomously by optimizing the activation of the neurons such that the resulting output data represent the actual measured values as accurately as possible.
For this type of information processing, the signals arriving at a neuron are first combined into an overall input value by using a propagation function (netk). The total input value is then processed by an activation function (f), which determines whether the neuron is activated. A common form of this activation function is the sum function, which calculates the total input value from the sum of weighted input signals.
A neuron is activated only if the calculated input value (net) is equal to or exceeds the specified value (oj). The weights (wjk) within the propagation function and the parameters of the activation function were adjusted during the learning process until the output data of the neurons represented the observed empirical data as accurately as possible.
After training, the model was validated using a separate dataset of P2 to assess its accuracy and generalizability. The validation was conducted by predicting the output data for a new set of input data previously unknown to the network, including their spatial positions. The evaluation can be seen in Fig. 3. The performance of the model in this task provides insight into how well it has learned to understand the relationship between data and spatial information and to apply this understanding to new, unknown data.
4. Discussion
In the initial investigations of a numerical sensor for stiffening glass façades, the analysis model used proved to be appropriate. Not only was there a significant correlation with the validation datasets, but divergences between the measured sensor data were also revealed. In particular, the data from displacement transducer 1 showed striking deviations, which were verified by analysis using an ANN. Therefore, the possibility of a hybrid monitoring system combining real and virtual load-bearing glass façades is feasible. However, at this point, it is important to emphasize the precision with which the sensor positions are determined. Accurate localization is essential for the ANN to be effective in pattern recognition and for the numerical sensors to be adequately trained on this basis. It is suggested that the positioning of real measurement systems be recorded using 3D measurement technology to determine the measurement points with the highest possible accuracy. Even small deviations of the virtual model from physical reality can have a significant impact on the results of the numerical sensors.
5. Conclusion
This paper introduces the concept of a numerical sensor as a key element for creating a hybrid digital twin focused on the monitoring of load-bearing glass façades. This study highlights the integration of numerical and physical sensors to optimize the accuracy and reliability of structural assessments of load-bearing glass façades. The analysis of empirical data and the subsequent development of a numerical model will not only deepen the understanding of redundancies in glass façades but also provide a basis for future safety strategies in such systems.
In addition, the integration of 3D measurement technologies will be implemented in future research to minimize the differences between virtual models and their real counterparts, thus increasing the accuracy of numerical sensors.
Furthermore, as the research progresses, the aim is to expand the data basis for training numerical models, investigate more complex data analysis algorithms, and improve the model's ability to adapt to new and unexpected conditions to predict damage scenarios on stiffening glazing more precisely.The future goal is to reliably predict the load scenarios of complex structures of stiffening glass façades.
Acknowledgements
This research paper is funded by dtec.bw - Digitalization and Technology Research Center of the Bundeswehr which we gratefully acknowledge. dtec.bw is funded by the European Union -NextGenerationEU.
References
Backhaus, K.; Erichson, B.; Weiber, R.: Fortgeschrittene multivariate Analysemethoden. Eine anwendungsorientierte Einführung. 3., überarbeitete und aktualisierte Auflage. Berlin, Heidelberg: Springer Gabler (2015).
Becker, T.; Krause, D.: Softsensorsysteme – Mathematik als Bindeglied zum Prozessgeschehen. In: Chemie Ingenieur Technik 82 (4), S. 429–440 (2010). DOI: 10.1002/cite.201000015.
Becker, T.; Weisbrich, S.; Euteneuer, F.; Wu, C.; Neitzel, F.: Neue Möglichkeiten in der Bauwerksüberwachung durch integrierte Analyse von Sensormessungen und 3D-Bauwerksmodell. In: Gemeinsame Tagung 2014 der DGfK, der DGPF, der GfGI und des GiN (DGPF Tagungsband 23).
Böhmer, H.; Brinkmann-Wicke, T.; Sell, S.; Simon, J.; Tebben, C. (Hg.): VHV-Bauschadenbericht. Hochbau 2021/22 : Qualität und Kommunikation. VHV Vereinigte Hannoversche Versicherung a.G.; Fraunhofer IRB-Verlag. Stuttgart: Fraunhofer IRB Verlag (2022). http://www.irbnet.de/daten/rswb/22039010315.pdf.
Fadai, A.; Winter, W.: Aussteifende Holz-Glas-Fassaden – Aussteifungssysteme und Nachweise. In: Glasbau 2014. 1. Auflage. Herausgegeben von Bernhard Weller, Silke Tasche.
Farrar, C.; Worden, K.: An introduction to structural health monitoring. In: Philosophical transactions. Series A, Mathematical, physical, and engineering sciences 365 (1851), pp. 303–315 (2007). DOI: 10.1098/rsta.2006.1928.
Fortuna, L., Graziani, S., Rizzo, A., Xibilia, M.G.: In: Soft Sensors for Monitoring and Control of Industrial Processes. Springer London (2007). https://doi.org/10.1007/978-1-84628-480-9.
Haese, A.: Beitrag zur Bemessung scheibenbeanspruchter Stahl-Glas-Elemente. Dissertation. Universität der Bundeswehr München, Neubiberg. Institut für konstruktiven Ingenieurbau (2013).
Hering, E.: Sensoren in Wissenschaft und Technik. Funktionsweise und Einsatzgebiete. Unter Mitarbeit von Gert Schönfelder. Wiesbaden: Springer Vieweg. in Springer Fachmedien Wiesbaden GmbH (2012). https://ebookcentral.proquest.com/lib/kxp/detail.action?docID=885622.
Hochhauser, W.: Ein Beitrag zur Berechnung und Bemessung von geklebten und geklotzten Holz-Glas Verbundscheiben. Dissertation. Technische Universität, Wien. Institut für Architekturwissenschaften (2011).
Homberg, W.; Arian, B.; Arne, V.; Borgert, T.; Brosius, A.; Groche, P. et al.: Softsensors: key component of property control in forming technology. In: Prod. Eng. Res. Devel (2023). DOI: 10.1007/s11740-023-01227-1.
Kadlec, P., Gabrys, B., Strandt, S.: Data-driven soft sensors in the process industry. Comput. Chem. Eng. 33 (4), 795–814 (2009). https://doi.org/10.1016/ j.compchemeng.2008.12.012.
Krawtschuk, A.; Strauß, A.; Haider, K.; Zimmermann, T.; Bergmeister, K.: Ermittlung von Modellunsicherheiten bei Stahlbetonstrukturen. In: Beton- und Stahlbetonbau 107 (12), pp. 824–835 (2012). DOI: 10.1002/best.201200053.
Maier, D.; Stebner, S.; Ismail, A.; Dölz, M.; Lohmann, B.; Münstermann, S.; Volk, W.: The influence of freeform bending process parameters on residual stresses for steel tubes. In: Advances in Industrial and Manufacturing Engineering 2, S. 100047 (2021). DOI: 10.1016/j.aime.2021.100047.
Neumer, D.: Beitrag zur Aussteifung von Gebäuden durch Glas – Konzentrierte Lasteinleitung im Eckbereich. Dissertation. Universität der Bundeswehr München, Neubiberg. Institut für konstruktiven Ingenieurbau (2018).
Stebner, S.; Maier, D.; Ismail, A.; Dölz, M.; Lohman, B.; Volk, W.; Münstermann, S.: Extension of a Simulation Model of the Freeform Bending Process as Part of a Soft Sensor for a Property Control. In: KEM 926, pp. 2137–2145 (2022). DOI: 10.4028/p-d17700.
Tomažič, S. Intelligent Soft Sensors. In: Sensors (Basel, Switzerland) 23, 15 (2023). DOI: 10.3390/s23156895.
Yuan, X.; Zhou, J.; Huang, B.; Wang, Y.; Yang, C.; Gui, W.: Hierarchical Quality-Relevant Feature Representation for Soft Sensor Modeling: A Novel Deep Learning Strategy. In: IEEE Trans. Ind. Inf. 16 (6), S. 3721–3730 (2020). DOI: 10.1109/TII.2019.2938890.
Zurawski, N.: Technische Innovationen und deren gesellschaftliche Auswirkungen im Kontext von Überwachung. Berlin: Freie Univ. Berlin FB Mathematik und Informatik Forschungsforum Öffentliche Sicherheit, Schriftenreihe Sicherheit, 16 (2015).